В.М. Дубровин, Т.А. Бутина
2
1
.
Et
K
e
E
(2)
Отношение
K
E
называется временем запаздывания деформации.
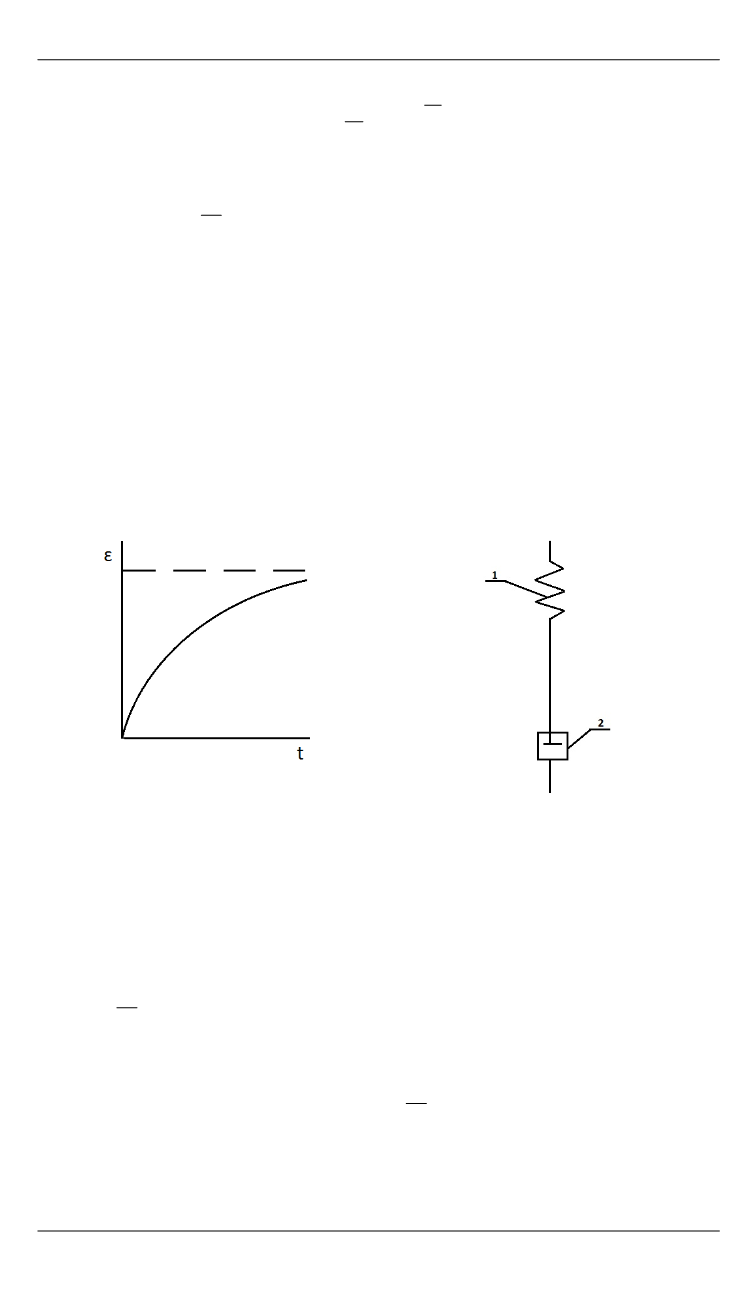
Зависимость деформации ползучести от времени для рассматривае-
мой модели в соответствии с формулой (1) представлена на рис. 2.
Если упругий и пластический элементы соединены последова-
тельно (рис. 3) модель называется моделью Максвелла. В этом случае
напряжение в обоих элементах одинаково, а деформации различны,
тогда справедливы следующие соотношения:
п
п
,
K
y
y
y п
,
,
E
где ε
у
, ε
п
– деформация упругого и пластического элементов соответ-
ственно.
Рис. 2.
Деформация ползучести
для модели Фойгта
Рис. 3.
Модель Максвелла
1
– упругий элемент;
2
– пластический
элемент
Исключив ε
у
и ε
п
, получим
,
n K
(3)
где
K n
E
– постоянная величина, называемая временем релаксации.
В случае σ = const из соотношения (3) получим
0
.
t
K
(4)
Зависимость деформации ползучести от времени для рассмот-
ренной модели в соответствии с (4) представлена на рис. 4.


