Спектральные кроссоверы в фотонном кристалле
5
При анализе возможности существования более сложного СК на ос-
нове равенства (11) установили, что в незаполненном ФК нет. Однако
этот сложный СК (тройное пересечение ветвей дисперсионных кри-
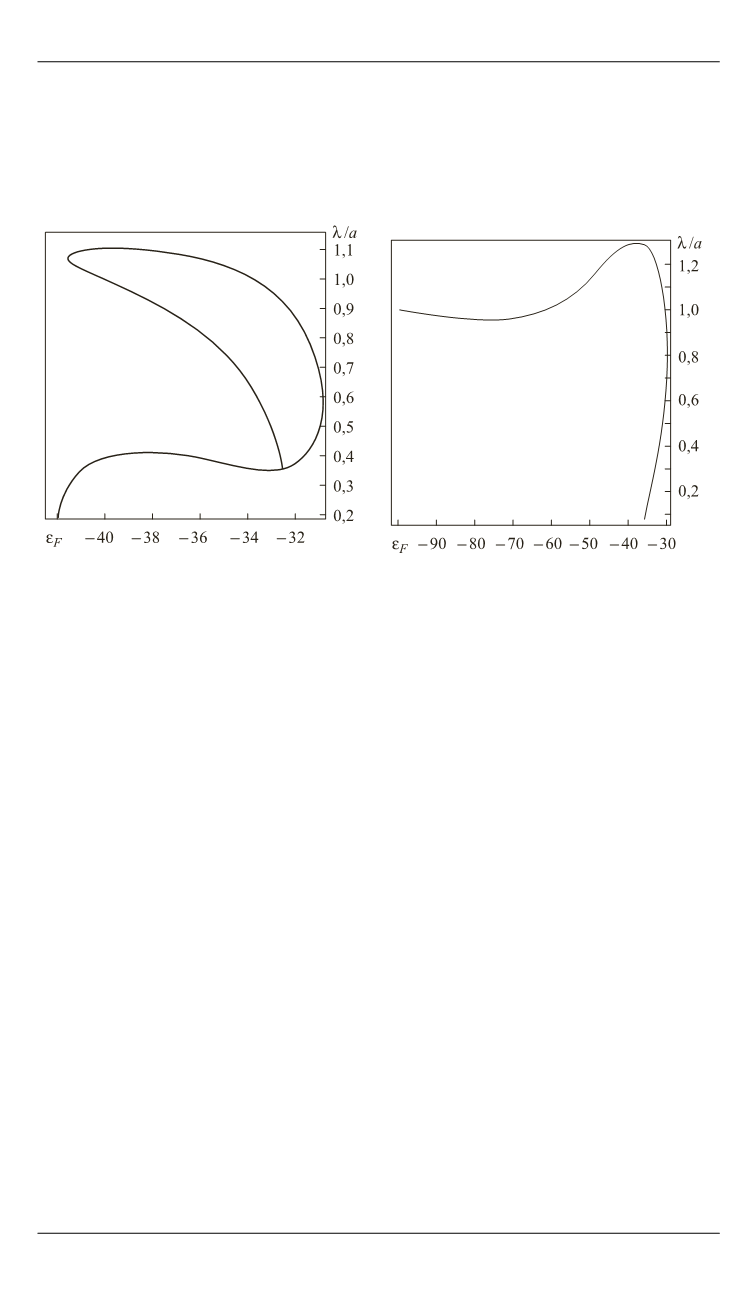
вых) может существовать при каскаде обычных СК. Числовой анализ
этой возможности иллюстрирует рис. 2.
Заключение.
Найдено уравнение для определения каскада СК
(пересечений более двух спектральных кривых) в ФК способами чис-
лового моделирования для опаловой матрицы без включений доказа-
но отсутствие СК. Для этой матрицы с включениями, имеющими от-
рицательное значение диэлектрической функции, определена область
СК. Путем численного моделирования для ФК с включениями обна-
ружена область существования более сложного СК, которому соот-
ветствует тройное пересечение дисперсионных ветвей, и доказано ее
отсутствие, если в ФК нет включений. Теория СК распространяется
на ФК, т. е. среду с периодической модуляцией диэлектрической
функции.
ЛИТЕРАТУРА
[1] Patton C.Е. Classical Theory of Spin-wave Dispersion for Ferromagnetic Met-
als.
Czech. J. Phys
, 1976, B26, pp. 925–935.
[2] Fraitova D. On the Analytical FMR Theory in the Normal Configuration.
Phys.
Stat. Sol.
(
b
), 1995, vol. 187, pp. 217–224.
Рис. 1.
Зависимость отношения длины
волны излучения при СК к постоянной
решетки
/
a
от диэлектрической функ-
ции включения
F
в ФК на основе ис-
кусственного опала
Рис. 2.
Зависимость отношения длины
волны излучения при сложном СК
(тройное пересечение дисперсионных
ветвей) к постоянной решетки
/
a
от
диэлектрической функции включения
F
в ФК на основе искусственного
опала СК


