А.С. Романов, А.В. Семиколенов
8
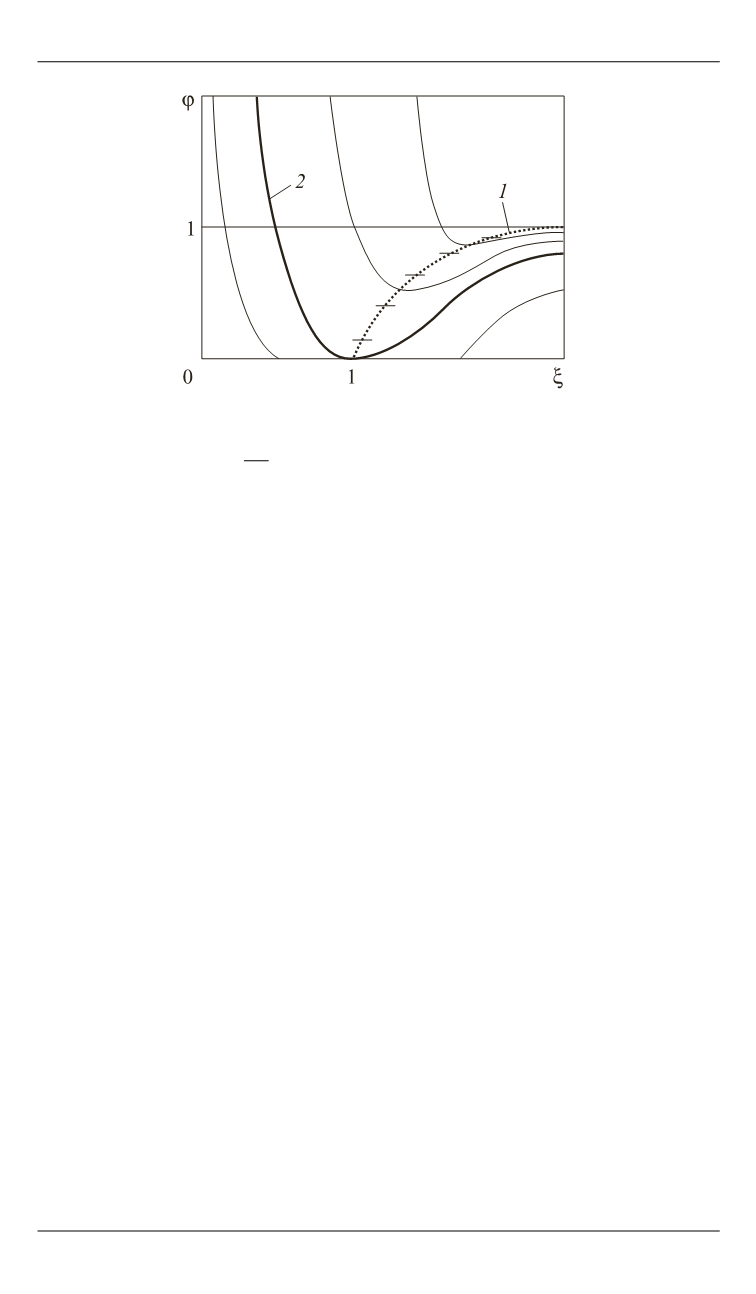
Рис. 2.
Качественный вид интегральных кривых уравнения (10):
1
– кривая, на которой
0
d
d
;
2
– интегральная кривая, на которой выполнено
граничное условие
= 0 при
= 1
Заключение.
Таким образом, в рамках развиваемой теории уда-
ется непротиворечиво описать переходный слой между
-пленкой и
объемной частью жидкости. Причем, как показано для объемной ча-
сти жидкости, выполняется условие Юнга. Принципиально важно,
что учет структурной составляющей расклинивающего давления
приводит к формальной задаче математической физики, для которой
область изменения толщин жидкости оказывается «отграниченной»
от твердой поверхности, т. е.
h
> 0, что существенно упрощает прове-
дение численных экспериментов по гидродинамике растекания при
смачивании.
ЛИТЕРАТУРА
[1]
Пухначев В.В., Солонников В.А. К вопросу о динамическом краевом угле.
ПММ
, 1982, т. 46, № 6, с. 961–971.
[2]
Романов А.С. Об одном способе гидродинамического описания растекания
частично смачивающей жидкости по плоской твердой поверхности.
КЖ
,
1990, т. 52, № 1, с. 93–99.
[3]
Дерягин Б.В., Чураев Н.В.
Смачивающие пленки
. Москва, Наука, 1984, 160 с.
[4]
Дерягин Б.В., Чураев Н.В., Мулер В.М.
Поверхностные силы
. Москва,
Наука, 1985, 399 с.
[5]
Жен П.Ж. Смачивание: статика и динамика.
УФН
, 1987. т. 151, № 4,
с. 619–681.
[6]
Miller C.A., Rukenshtein E. The Origin of Flow during Wetting of Solids.
J.
Col
.
Interface Sci
., 1974, vol. 48(3). pp. 368–373.
[7]
Cerro M.C.G. del, Jameson G. Theory for Equilibrium Contact Angle Between
a Gas, a Liquid and Solid.
J. Chem. Soc. Faraday Trans. I
., 1976, vol. 72,
pp. 883–895.


