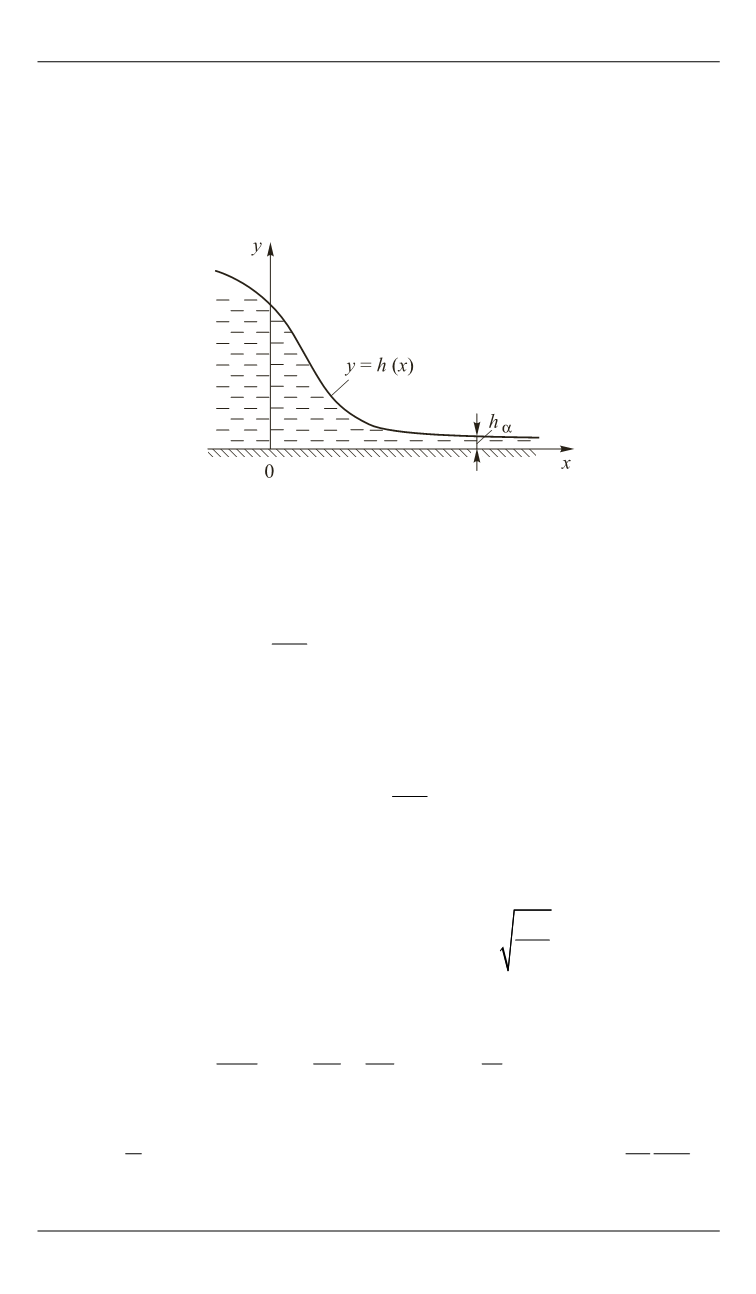
Форма свободной поверхности жидкости, находящейся в равновесии
5
Для определенности рассмотрим форму поверхности жидкой
пленки, свободно лежащей на горизонтальной плоской твердой по-
верхности, и выберем систему координат, как указано на рис. 1. В этой
системе координат уравнение
( )
y h x
определяет форму свободной
поверхности жидкости.
Рис. 1.
Форма свободной поверхности
Функция
h
(
x
) определяется из уравнения, которое следует из ме-
ханического условия равновесия:
2
2
,
,
l
h gh
h C
x
(6)
где
0
C
– некоторая постоянная;
l
– плотность жидкости;
g
–
ускорение свободного падения; в рассматриваемом приближении
кривизна поверхности пленки
2
1
2
.
h
x
Изучение равновесия жидкой пленки удобно провести в безраз-
мерных переменных. При этом более определенно выясняется роль
отдельных слагаемых в соотношениях (5) и (6). Выберем в качестве
характерной величины характерную длину
l
L
g
(так называемая
капиллярная длина). Тогда уравнения равновесия (6) принимают вид
4
2
4 1
2
3
,
e
k
d w R dw
w
C
dx
w
dx
w
(7)
где
h w
L
– безразмерная толщина жидкой пленки;
2
48
LL
A R
L
–
безразмерный критерий, определяет относительную роль расклини-


