В.П. Печников
6
Выражения (7) для радиальной и окружной деформации прини-
мают вид
2
2
0
2
2
к
к
к
к
к
к
к
к
2
2
0
2
2
;
1
1 2
1
1
1 2
1
.
r
z
z
r
p m q q p
r
E m
r
p m q q p
r
E m
(10)
Оболочка корпуса выполнена методом намотки. Считается, что
композиционный материал обладает ортотропными механическими
характеристиками, которые можно определить [8–10]. Закон Гука для
такой оболочки с учетом температурных деформаций имеет вид
1
1
1 2
1
0
1
2
2
2 1
2
0
2
1
;
1
(
),
Т Т
E
Т Т
E
(11)
где
1
,
1
,
2
,
2
— деформации и напряжения вдоль образующей
оболочки (индекс «1») и в ее окружном направлении (индекс «2»);
1 1 2 2
, , ,
E E
— соответствующие модули упругости и коэффициент
Пуассона материала оболочки;
1
,
2
— коэффициенты линейного
расширения ортотропной оболочки в осевом и окружном направле-
нии соответственно.
Оболочка находится под действием
внутреннего контактного давления
к
q
со стороны заряда и осевых сил. Темпе-
ратурные деформации, как и раньше, не
учитываем. Окружное напряжение име-
ет вид
1
2
,
к
q r
(12)
а осевое напряжение находим из усло-
вий равновесия отсеченной части обо-
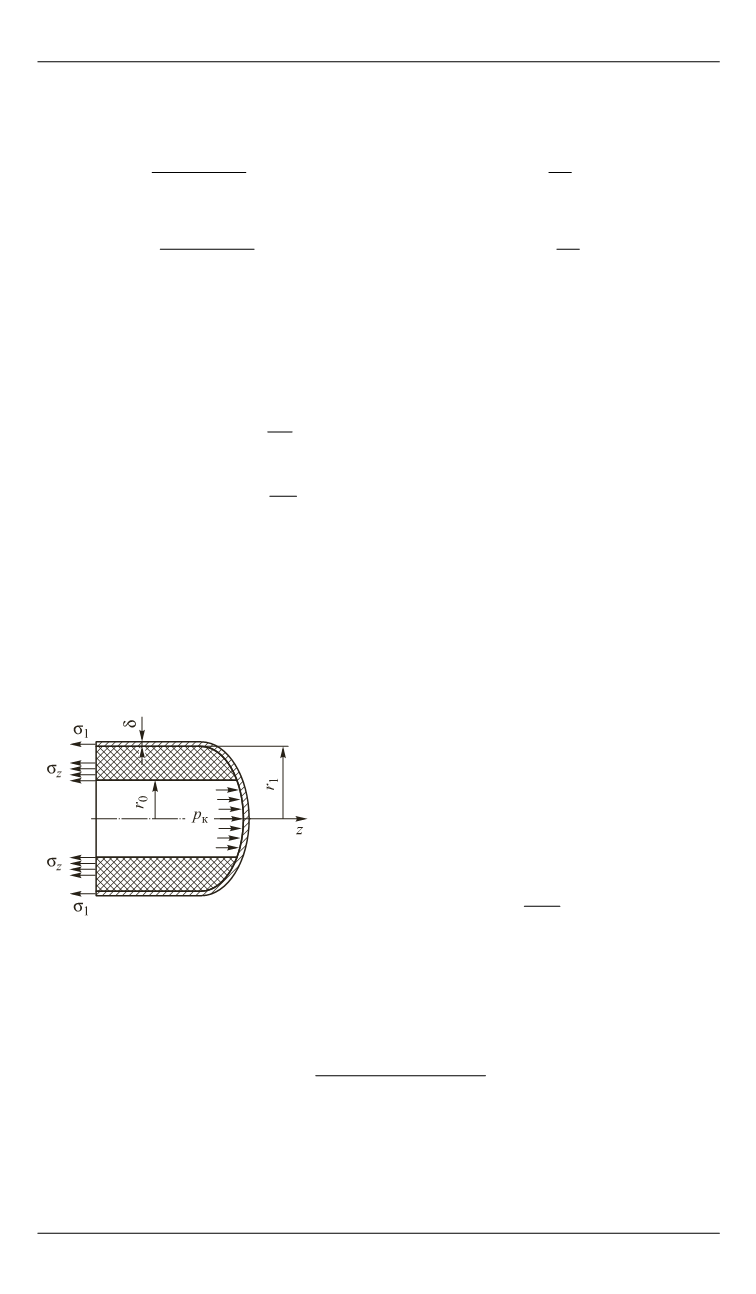
лочки и заряда (рис. 4):
2
2
2
к 0
1
0
1
1
.
2
z
p r
r r
r
(13)
На границе оболочки и заряда при
1
r r
выполняются условия
совместности осевой и окружной деформаций:
1
;
z
2
.
Рис. 4.
Напряжения в заряде и
оболочке в отсеченной части
двигателя
при
действии
внутреннего давления


