4
Е.В. Смирнов
руют из образца в зонд. Сила тун-
нельного тока зависит от напряже-
ния смещения
U
, коэффициента
прозрачности барьера и плотности
состояний электронов вблизи уров-
ня Ферми.
В случае, когда напряжение
U
невелико (энергия
eU
меньше рабо-
ты выхода электрона из металла),
выражение для плотности туннель-
ного тока можно представить в
виде [1]:
0
cp
2 exp
2
.
e
j j U
m A z
(1)
Здесь
m
e
— масса электрона,
cp
2
B B
A A
A
; Δ
z
— ширина потенциального барьера между острием
поверхностью. В (1) считается, что предэкспоненциальный множитель
j
0
(
U
) не зависит от расстояния Δ
z
, а только от напряжения
U
. При ха-
рактерных значениях работы выхода
А
ср
~ 4 эВ константа затухания в
экспоненте
cp
2 2
20
e
m A
нм
–1
. Тогда из (1) следует, что при измене-
нии Δ
z
на ~ 0,1 нм, величина туннельного тока меняется примерно на
порядок, что и обусловливает очень высокую разрешающую способ-
ность СТМ. Вдоль оси
z
, перпендикулярной поверхности образца, раз-
решающая способность достигает значения δ
z
~ 10
–3
нм = 1пм, а вдоль
осей
x
и
y
, параллельных поверхности образца, — δ
x
, δ
y
~ 10
–2
нм. Такое
высокое разрешение СТМ позволяет с его помощью проводить деталь-
ное исследование отдельных атомов, находящихся на проводящей по-
верхности.
Реальный потенциальный барьер между острием СТМ и исследуе-
мой поверхностью не является одномерным, как в рассмотренном выше
случае, а имеет более сложную структуру. Тем не менее и в общем
случае выявленная основная особенность туннелирования — экспо-
ненциальная зависимость туннельного тока от расстояния Δ
z
между
зондом и образцом — сохраняется, что подтверждается результатами
экспериментов (рис. 4). Отметим, что сила тока
I
на рис. 4 отложена в
логарифмическом масштабе.
Следует отметить, что СТМ, в отличие от других электронных ми-
кроскопов, не содержит линз, и, следовательно, получаемое в нем изо-
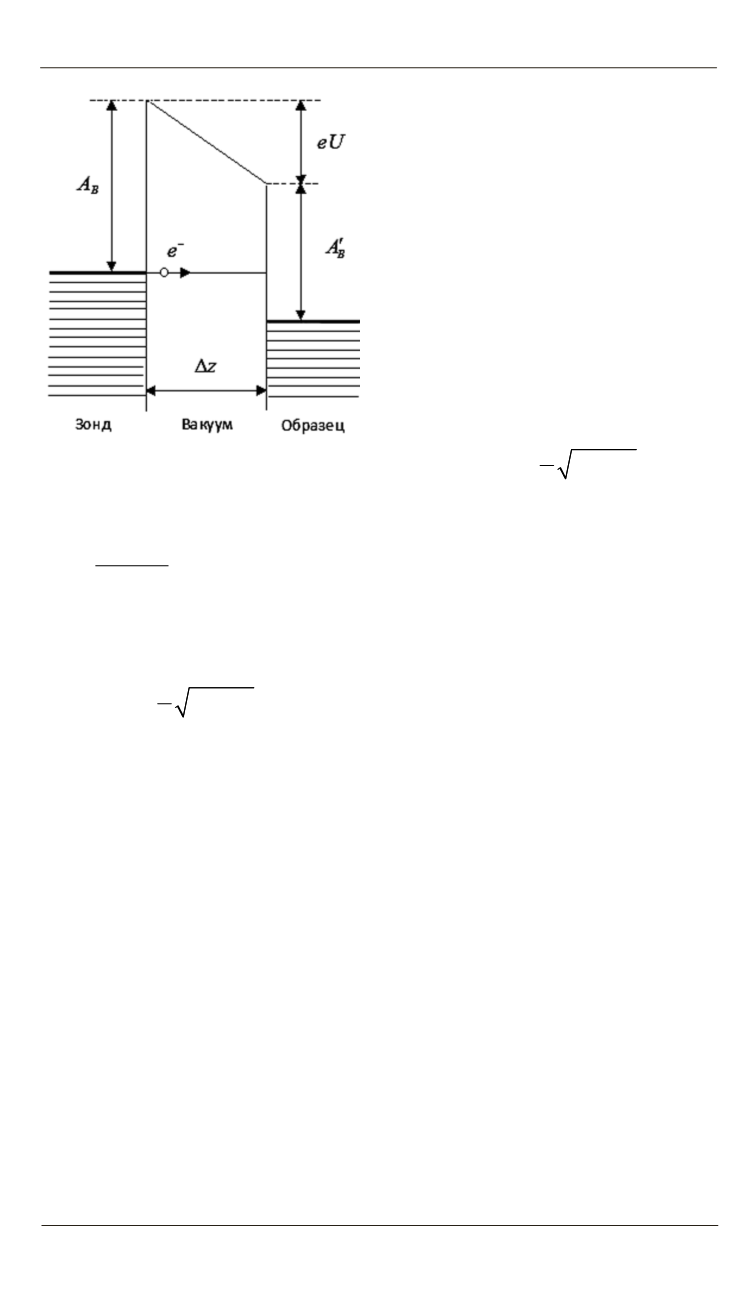
Рис. 3.
Диаграмма «туннельного
контакта» СТМ


