Неизменность основного допущения моделей переноса теплоты в контактах
7
в соответствии с фрактальной функцией Вейерштрасса—Мандельброта
[8], создавая модель шероховатой поверхности с
R
max
= 5 мкм.
На верхней поверхности тела А теплообмен проходит при
a
1
= 50 Вт/(м
2
· K);
Т
1г
= 330 K, а на нижней поверхности тела Б при
a
2
= 10 Вт/(м
2
·K) и
Т
2г
= 273 K. В области фактического касания тепло-
вой контакт считался идеальным. Из полученного расчетом темпера-
турного поля можно вычислить термическую проводимость контакта:
1 1
1
1 2
(
) .
w
T T
q
T T T
δ
α −
α = =
∆
−
г
Величины
Т
1
и
Т
2
определены как средние значения по верхнему
и нижнему сечениям на расстоянии
δ
от линии раздела контактиру-
ющих поверхностей. Для того чтобы ограничить область, в которой
температурное поле существенно трехмерно, принято
δ
= 25 мкм.
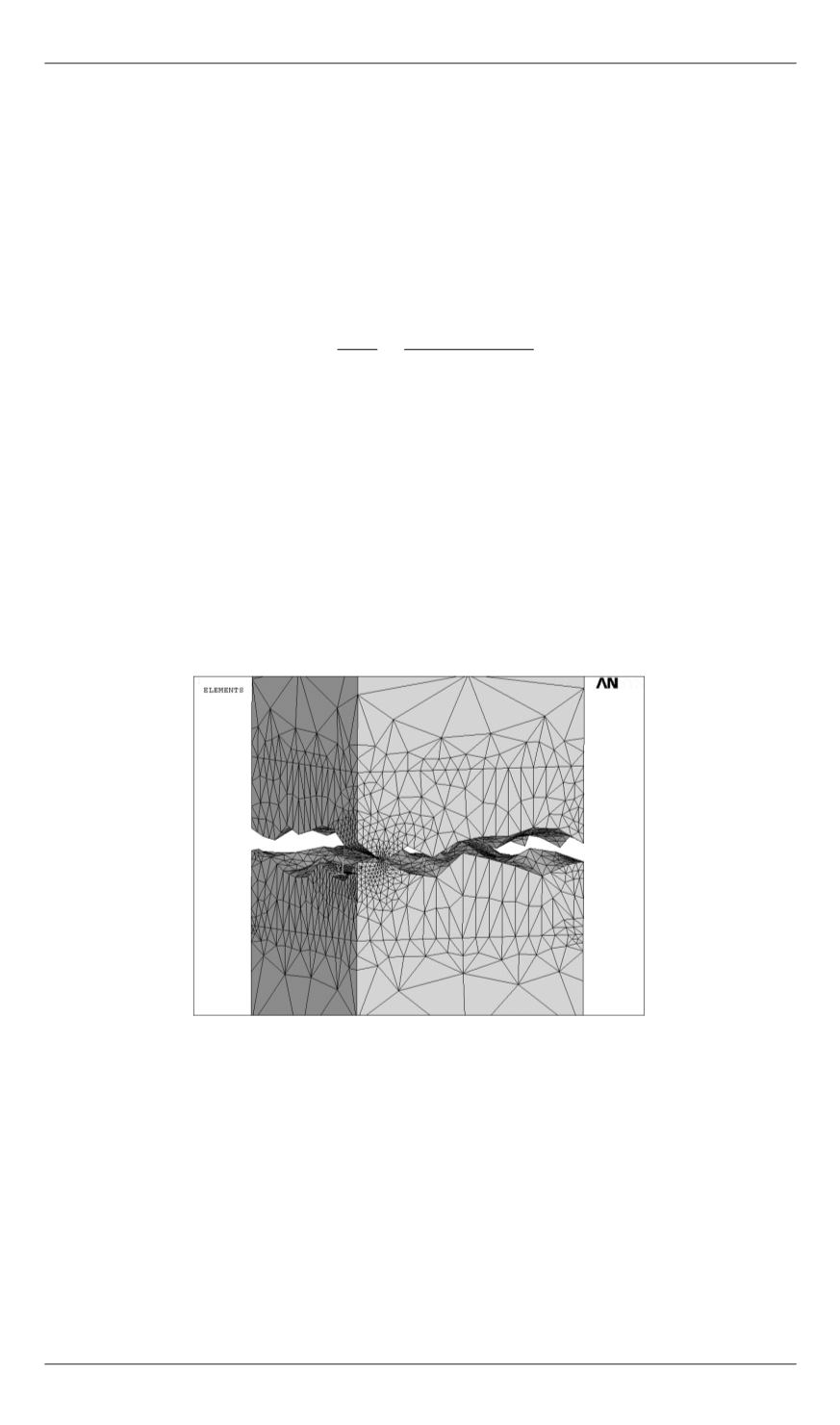
Нелинейная контактная задача решена в программном комплексе
конечно-элементного анализа ANSYS (рис. 5). Большое значение для
устойчивости геометрических расчетов имеет перевод размерности всех
величин из метров в миллиметры.
Рис. 5.
Пространственная конечно-элементная модель участка шероховатой
поверхности
Результаты вычисления фактической площади контакта для раз-
личных значений давления приведены ниже:
P
, МПа
2 10 30 60 120
Доля площади фактического контакта
в номинальной площади, %
0,04 0,18 0,69 1,63 2,98


