М.В. Мурашов, С.Д. Панин
2
ности приводит к использованию эмпирических зависимостей для соз-
дания аппаратов.
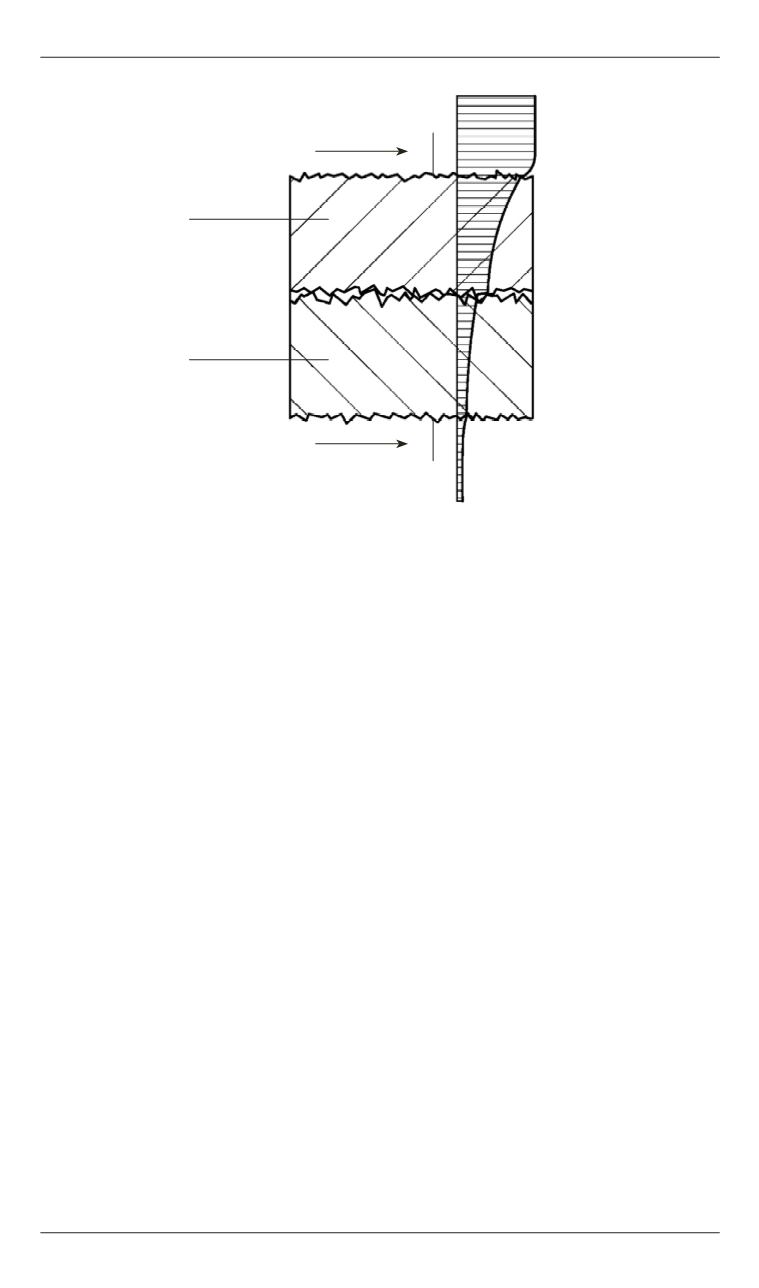
Сущность возникших проблем в переносе теплоты при контакте
шероховатых тел иллюстрирует наиболее простой случай теплопере-
дачи через металлическую конструкцию, состоящую из двух слоев раз-
личных материалов (рис. 1).
Внешняя задача.
Стационарный перенос теплоты конвекцией
в единицу времени от газа в слой А определяет классическое соотно-
шение [3]
1
0
,
F
Q
TdF
= α ⋅ ∆
∫
(1)
где
a
1
(
F
) — коэффициент конвективного теплообмена;
D
T
(
F
) =
=
T
1г
−
T
w
1
(
F
) — перепад температуры от значения в ядре потока газа
до значения на поверхности тела А;
F
— площадь теплообмена. При
отсутствии шероховатости поверхности используют номинальное зна-
чение площади и значения коэффициентов теплообмена для гладкой
стенки. Как быть при наличии шероховатости как на поверхностях
слоя А, так и слоя Б (см. рис. 1)? Определить истинную площадь шеро-
ховатой поверхности расчетным путем крайне трудно, поэтому обычно
наличие шероховатости учитывают только с помощью коэффициента
теплообмена, оставляя номинальное (гладкое) значение площади в урав-
нении (1).
А
T
w
1
a
1
a
2
T
w
2
T
2г
T
1г
Б
Рис. 1.
Схема переноса теплоты через двухслойную конструкцию


