Ю.М. Темис, Х.Х. Азметов, А.И. Факеев
=
⎧⎪⎪⎨ ⎪⎩
( ) (
q
,
)
e
*
,
e
*
6
e
*
,
( ) (
q
,
)
e
*
+ (
q
,
) (
q
,
)
×
×
[︁ (︁
e
+
e
*
−
e
*
(
q
,
)
,
)︁
−
s
( )
]︁
,
e
*
>
e
*
,
(2)
= 1
,
2
,
s
*
( ) = (
q
,
)
s
( )
,
e
*
=
(
q
,
)
(
q
,
)
e
.
где
s
*
и
e
*
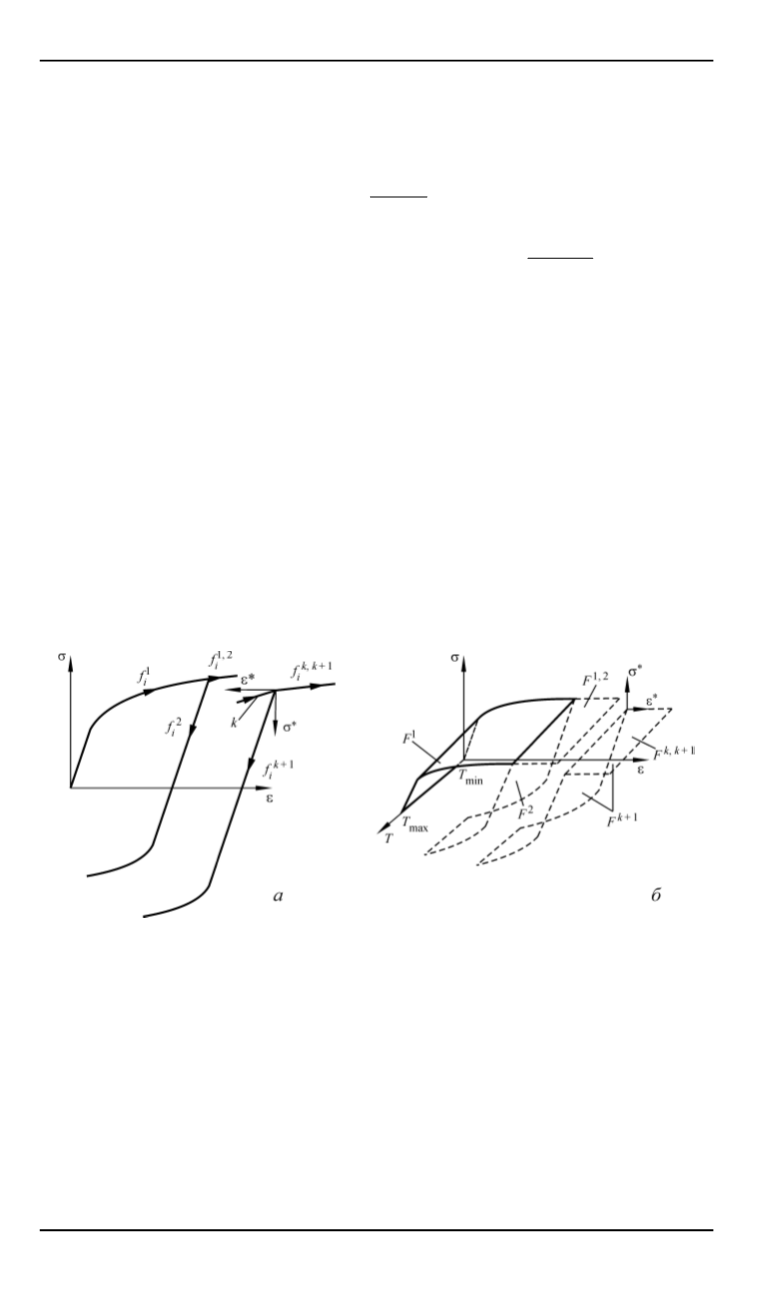
— напряжения и деформации в локальной системе коор-
динат полуцикла (рис. 1,
a
);
(
q
,
)
— размер упругой зоны поверхно-
сти нагружения;
(
q
,
)
— коэффициент преобразования нелинейного
участка первоначальной кривой деформирования;
(
q
,
)
— коэффи-
циент изменения модуля упругой разгрузки;
e
и
s
— деформации
и напряжения в пределе текучести первоначальной кривой;
( )
—
первоначальный модуль упругости;
(
e
,
)
— функция, описывающая
нелинейную часть термомеханической поверхности на первом полу-
цикле;
( )
— функция, описывающая кривую циклического дефор-
мирования, соответствующую температуре . Отметим, что
(
q
,
)
,
(
q
,
)
и
(
q
,
)
— зависящие от значения
q
параметры кривой цик-
лического деформирования, полученной по результатам циклических
испытаний при температуре .
Рис. 1.
Кривые изотермического циклического деформирования термомеханической
поверхности (
а
) и участок этой поверхности на различных полуциклах (
б
)
Для моделирования кривой деформирования при неизотермиче-
ском циклическом нагружении на каждом -м полуцикле нагруже-
ния необходимо построить изотермические кривые деформирования
+1
(рис. 1,
а
) в диапазоне температур текущего полуцикла. При этом
следует учесть накопленную пластическую деформацию
q
за преды-
дущие полуциклы; построить по полученным кривым деформирова-
ния термомеханическую поверхность текущего
( + 1)
-го полуцикла
+1
(рис. 1,
б
), на которой в пространстве напряжений, температур
2


