Исследование затрат характеристической скорости
7
исходит именно в точке
N
1
, которую можно рассматривать как точку
компромиссного значения продолжительности перелета. Рисунок 5
и формула (6) применимы для оценки оптимального времени ожидания
на фазирующей орбите путем нахождения точки пересечения кривой
затрат скорости с аналогичной кривой, получающейся для орбиты с вы-
сотой, близкой к заданной.
Задача перевода КА в целевую точку орбиты, имеющей суще-
ственное отклонение долготы восходящего узла.
В случае необходи-
мости перевода спутника на рабочую орбиту, имеющую существенное
отличие в ДВУ, затраты суммарной характеристической скорости на пе-
релет резко возрастают [5]. Выражение для оптимальных затрат суммар-
ной характеристической скорости для перевода КА в целевую точку ор-
биты с долготой восходящего узла, отличающейся на ΔΩ, имеет вид [3]
2
2
2
0
2
2 2 2
4
sin
2 (
) (3 (4 7 ) ) .
3 (
)
(
)
tg
i
u n
u n
V V
N n
N n
i
∆ +
∆Ω − ∆ + δΩ
∆ =
+
+
+ δΩ +
(7)
Здесь угол Δ
u
также выражен в долях витка, но его значения теперь
принимаются лежащими в интервале [0; 1];
n
— разница в числе витков
полета КА и целевой точки, в которую надо перевести КА [6].
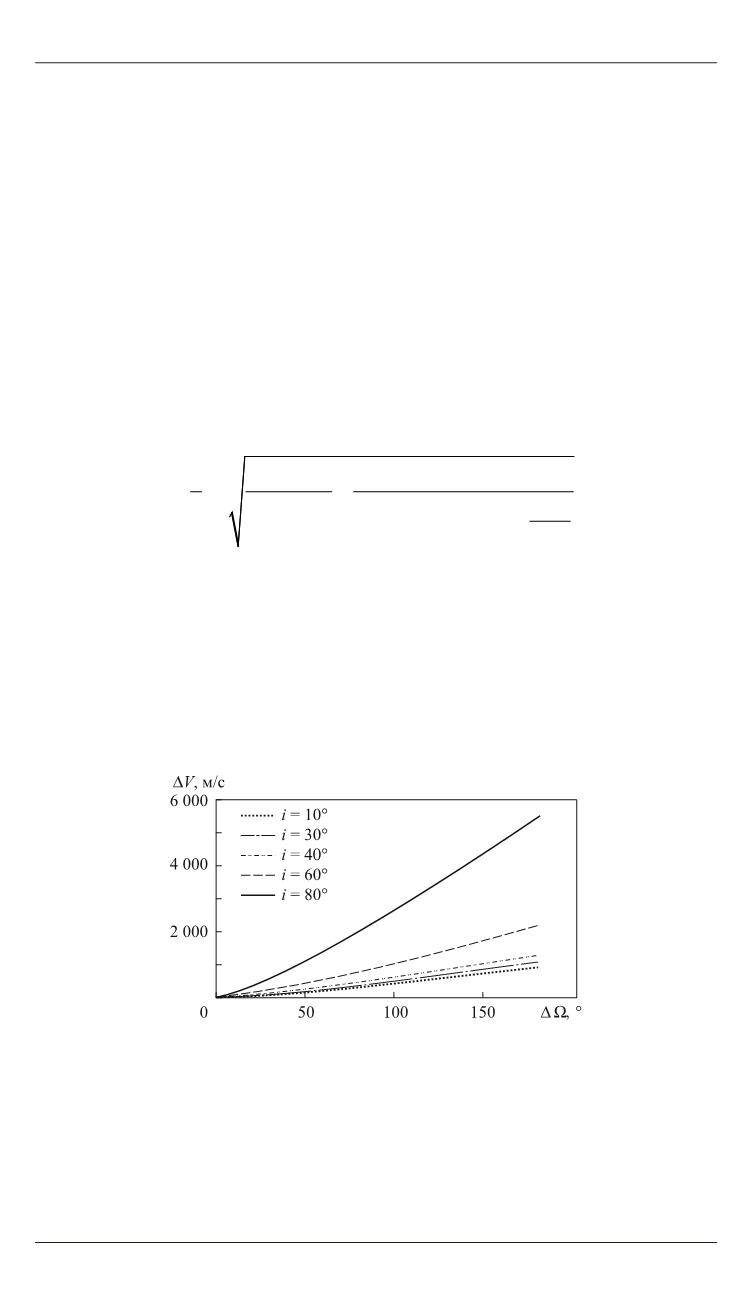
Зависимость затрат скорости от рассогласования в ДВУ близка к ли-
нейной, но существенно зависит от наклонения орбиты, причем интен-
сивность роста затрат резко возрастает в диапазоне значений
[60º ; 90º ]
i
∈
(рис. 6).
Рис. 6.
Зависимость затрат суммарной характеристической скорости
от рассогласования по ДВУ для разных наклонений для высоты 700 км
и
N
= 1000 витков
Влияние особенностей гравитационного поля Земли заметно про-
является в случае малых отклонений по ДВУ. На рис. 7 представлены
результаты расчетов для различных наклонений в малом диапазоне зна-


