А.А. Баранов, Д.А. Гришко, В.И. Майорова
4
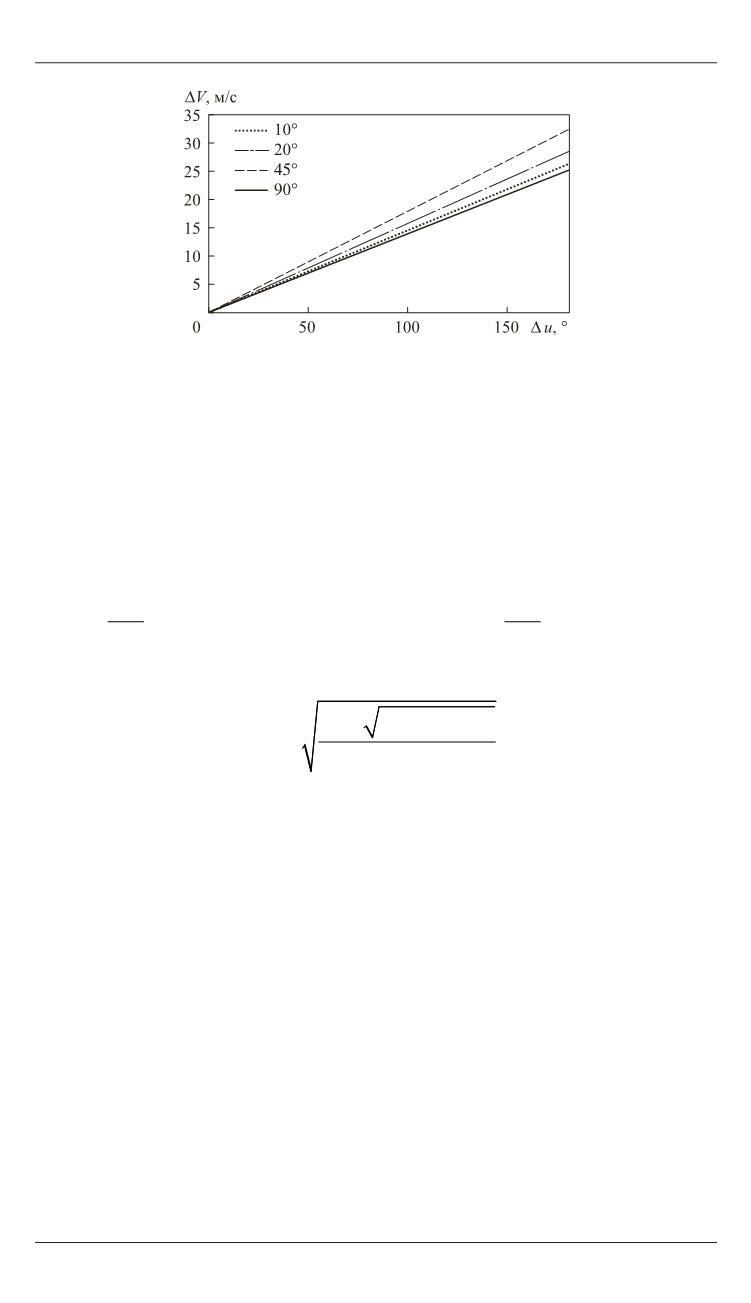
Рис. 3.
Зависимость затрат скорости от ∆
u
для различных наклонений
В формуле (4) наклонение может быть варьируемым параметром
при решении задач проектной баллистики. На рис. 3 приведены затраты
скорости для высоты 700 км, необходимые для устранения рассогласо-
вания по фазе для различных наклонений. Даный рисунок показывает,
что максимум затрат скорости приходится на значения, близкие к 45º,
а минимум — на полярные и экваториальные орбиты.
Исходя из формулы (4), нетрудно показать, что с учетом
2
2 cos ,
i
p
πε
δΩ = −
µ
или иначе δΩ = βcos
i
, где
2
2 ,
p
πε
β = −
µ
максимум затрат
суммарной характеристической скорости имеет место при наклонении
2 2
2 2
8 64 16
arcsin
.
2
N
i
N
− + + β
=
β
(5)
Так как β — функция фокального параметра, то, рассмотрев вари-
анты высот орбит 300, 700 и 20 000 км, можно констатировать, что,
в отличие от зависимости
i
от
N
зависимость
i
от
p
крайне слабая,
а точки
i
= 0 и
i
= π/2 являются точками минимума (рис. 4) и не зави-
сят от β.
Затраты суммарной характеристической скорости, требуемой для
перевода спутника в целевую точку орбиты, гиперболически зависят от
количества витков ожидания на промежуточной орбите для всех высот.
Рассмотрим изохронную зависимость по базовому числу витков для
высот 700 км и 2 500 км. Как видно из рис. 5, помимо существенного
рассогласования при малых
N
существует такая область значений
N
,
в которой кривые затрат суммарной характеристической скорости пере-
лета пересекаются.
Точке пересечения присуще резкое уменьшение абсолютного зна-
чения производной функции ∆
V
по переменной
N
, она может рассма-
триваться как некое компромиссное количество витков ожидания между


