А.А. Александров, Д.К. Драгун, А.И. Забегаев, В.В. Ломакин
4
Рассмотрение той же задачи в упругой постановке с использова-
нием метода конечных элементов (рис. 3) [3, 4] приводит к решению
следующей системы уравнений динамического равновесия:
{ }
{ }
{ }
{ }
( )
{ }
{ }
M
K
L
( )
( ) ,
i
i
i
t
h
h
′′
′
⋅
+
⋅
+ ⋅
=
′
=
⋅ ϕ +
+
∑
∑ ∑
q
q
q
Q
R
R
пр
выд
пр
выд
пр
выд
пр
где [M
пр
] — приведенная матрица масс (инерции), [M
пр
] = [M
11
] –
– [L
12
]∙[L
22
]
−1
∙[M
21
] – [M
12
]∙[L
22
]
−1
∙[L
21
] + [L
12
]∙[L
22
]
−1
∙[M
22
]∙[L
22
]
−1
∙[L
21
];
[K
пр
] — матрица демпфирования; [L
пр
] — приведенная матрица жест-
кости, [L
пр
] = [L
11
] – [L
12
] ∙ [L
22
]
−1
∙ [L
21
];
{ } { } { }
,
,
′
′′
q
q
q
выд
выд
выд
— со-
ответственно векторы перемещений, скоростей и ускорений по выде
ленным обобщенным координатам; {
Q
пр
}
i
— приведенный вектор сил,
зависящих от времени, {
Q
пр
} = {
Q
выд
} – [L
22
]
−1
∙ {
Q
ост
}; φ
i
(
t
) — временная
функция;
R
(
h
),
R
(
h ׳
) — соответственно векторы сил динамических эле-
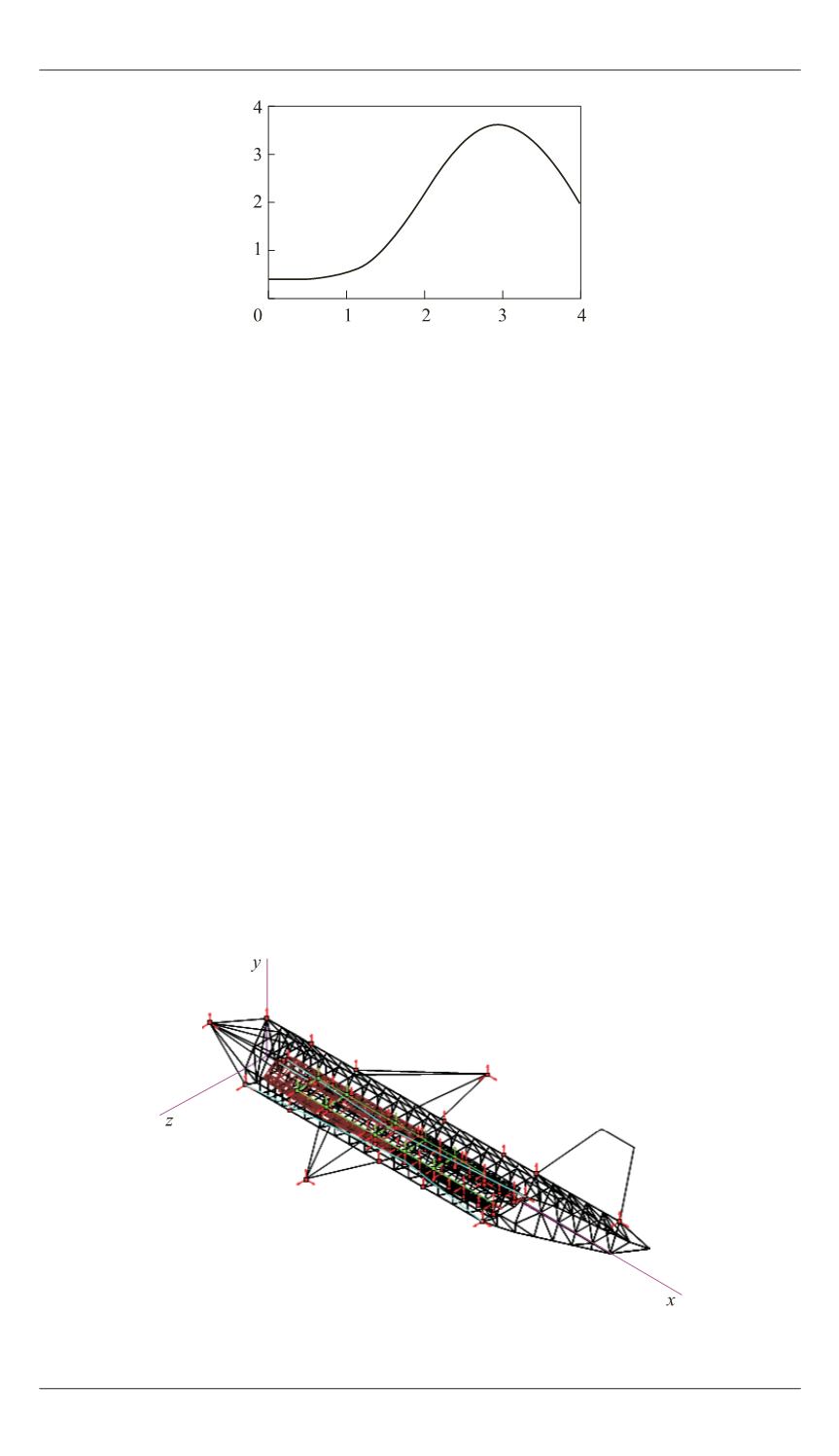
Рис. 2.
Угол атаки самолета-носителя при сбросе ракеты, град
Рис. 3.
Конечно-элементная расчетная схема самолета-носителя и ракеты


