
Е.А. Андреев, В.И. Крылов, А.В. Новиков, О.Е. Шацкий
4
Инженерный журнал: наука и инновации
# 1·2018
Значения
2
СН ж
n
и
к
d
необходимы для определения скорости ис-
парения капель в локальном объеме КС и источникового члена в
уравнении сохранения концентрации керосина.
Расчет характеристик испарения капель жидкого горючего (керо-
сина) проведен по методике, подробно изложенной в работе [3], в
соответствии со следующими ее положениями.
Малый сферический объем жидкости, заключенный в неограни-
ченной газовой среде, испаряется и затем исчезает. Необходимо со-
ставить уравнения и формулы, отражающие влияние свойств жидко-
сти, пара и атмосферы на продолжительность испарения.
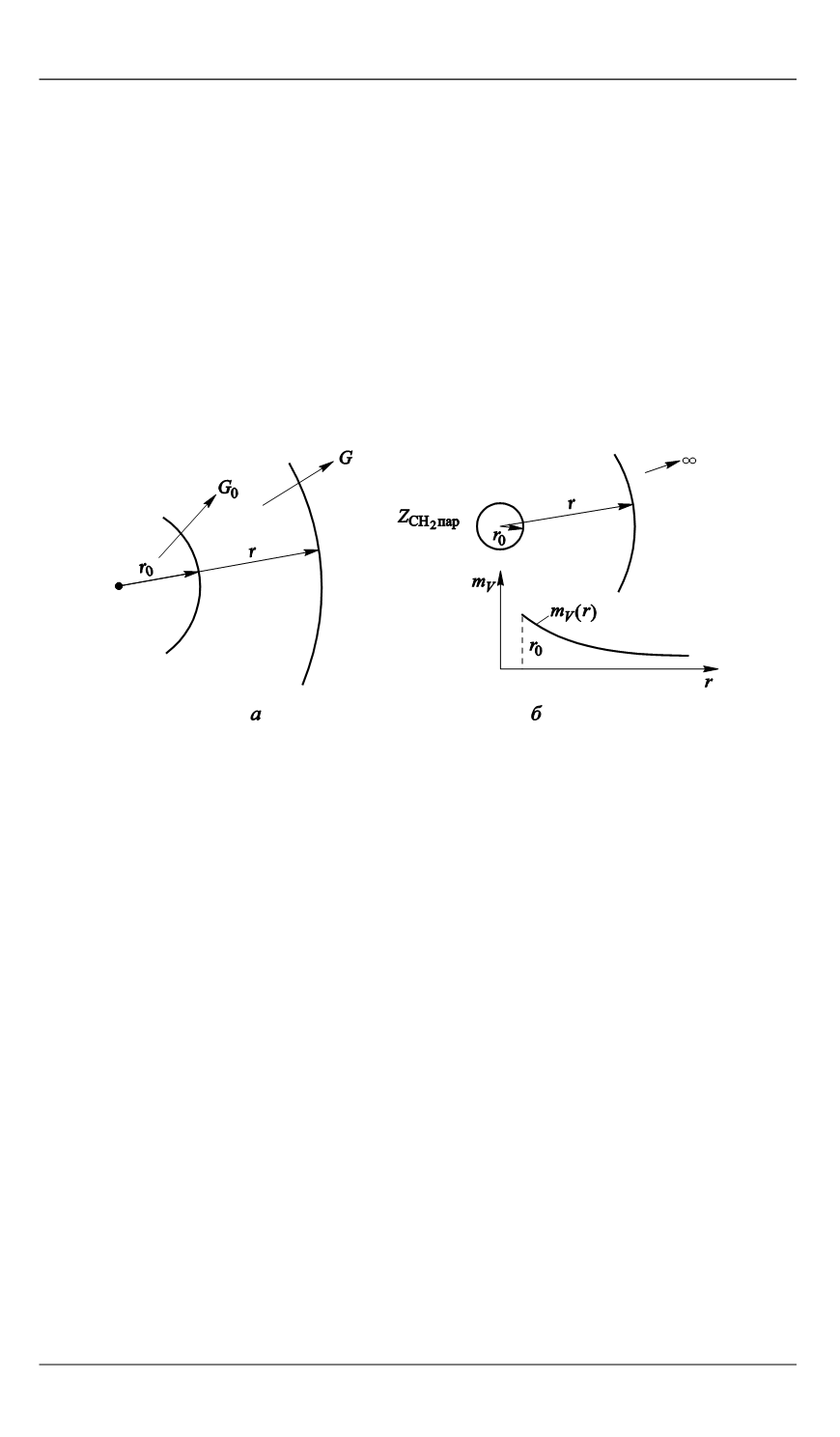
Математическая модель испарения капли представлена на рис. 3.
Рис. 3.
Математическая модель испарения капли:
а
— закон сохранения массы;
б
— общий характер распределения концентрации
пара вблизи поверхности частицы
В модели испарения капли протекающие процессы описываются
в сферически симметричной системе координат (при пренебрежении
нерадиальным движением) и рассматриваются в стационарной по-
становке. Считается, что значение коэффициента массообмена не
зависит от радиуса капли и расстояние между каплями велико.
Выполним расчет распределения концентрации пара
2
CH пар
z
в га-
зовой среде.
Из закона сохранения массы (рис. 3,
а
) следует
2
2
0 0
,
Gr G r
=
(3)
где
G
— поток массы на расстоянии
r
от центра капли;
G
0
— ско-
рость фазового превращения жидкости на единице площади поверх-
ности;
r
0
— радиус поверхности капли.
Поскольку химической реакции у поверхности капли не происхо-
дит, то
2
2
2
пов. пар
ов. пар0 0
0 0
.
п
G r G r G r
=
=
(4)
















