
О.А. Штейнбрехер, Т.В. Бурнышева
8
Инженерный журнал: наука и инновации
# 10·2017
«Композит-НК» [7, 8] на основе дискретной модели [9]. Для модели-
рования конструкции использовались конечные элементы типа балки
Тимошенко, приложение нагрузки моделировалось с использованием
«жесткого» узла [10].
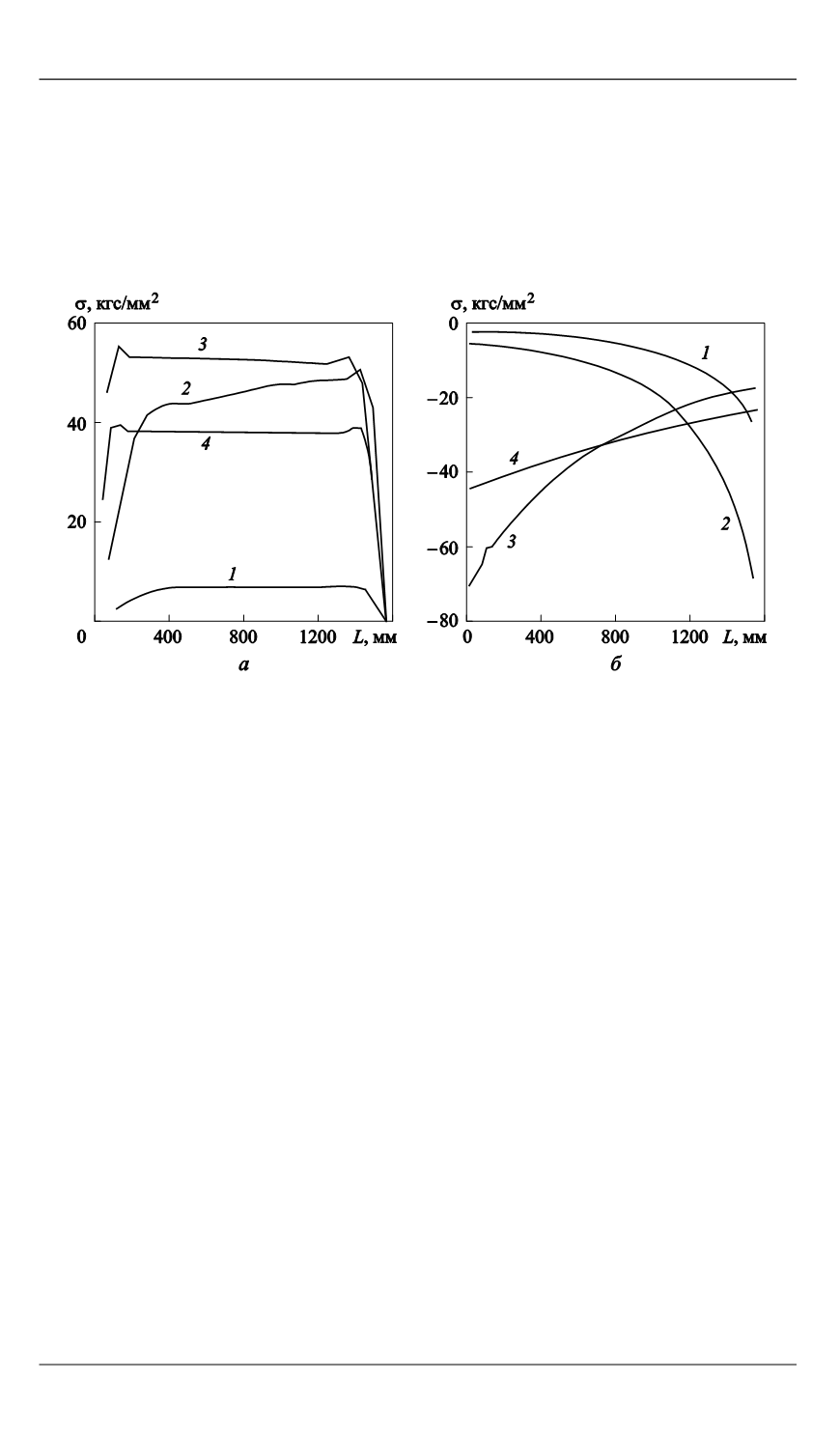
На рис. 5 представлены распределения напряжений в спиральных
и кольцевых ребрах конструкции по высоте.
Рис. 5.
Распределения напряжений в ребрах конструкции:
а
— кольцевые;
б
— спиральные ребра;
1
— аналитические зависимости по выбору оптимальных
параметров;
2
— циклический перебор по аналитическим зависимостям;
3
— симплексный поиск
[3] с фиксированным числом спиральных ребер;
4
— симплексный поиск [3]
Расхождения с результатами, представленными в работе [6], обу-
словлены тем, что значение ширины сечения кольцевого ребра, ис-
пользуемого при расчете сжимающей силы, при оптимальном проек-
тировании заменено его выражением из площади сечения кольцевого
ребра, рассчитанного с учетом приложенной нагрузки и предела
прочности кольцевых ребер. Кроме того, в работе [6] не представле-
ны все физико-механические параметры материала, и формулы [1] не
учитывают ограничения по жесткостям, принятые в расчетах [6].
Вывод.
Рассмотрено применение симплексного алгоритма по
аналитическим формулам и проведено сравнение полученного ре-
зультата с вычислениями методом перебора. Для учета большего
числа ограничений, например, ограничений по жесткостям, и более
точного представления ограничений по устойчивости и прочности в
качестве функций ограничений симплексного алгоритма [3] также
можно использовать аппроксимационные зависимости, полученные в
ходе вычислительного эксперимента [11]. Для обеспечения физиче-
ского смысла задачи данные функции должны быть представлены в
виде обратных зависимостей.
















