
Решение задачи параметрической оптимизации сетчатой цилиндрической конструкции
Инженерный журнал: наука и инновации
# 10·2017 7
С учетом антиградиента целевой функции оптимум находится в точке с
координатами (38,5; 49), доминантным ограничением является местная
устойчивость конструкции. При варьировании четырех проектных па-
раметров (при вычислении площади кольцевых ребер исходя из предела
прочности ребер) алгоритм симплексного поиска дает следующий ре-
зультат: угол наклона спирального ребра к образующей 38,67
°
, число
пар спиральных ребер 48,86, высота сечения ребра 3,13 мм и ширина
спирального ребра 5,234 мм.
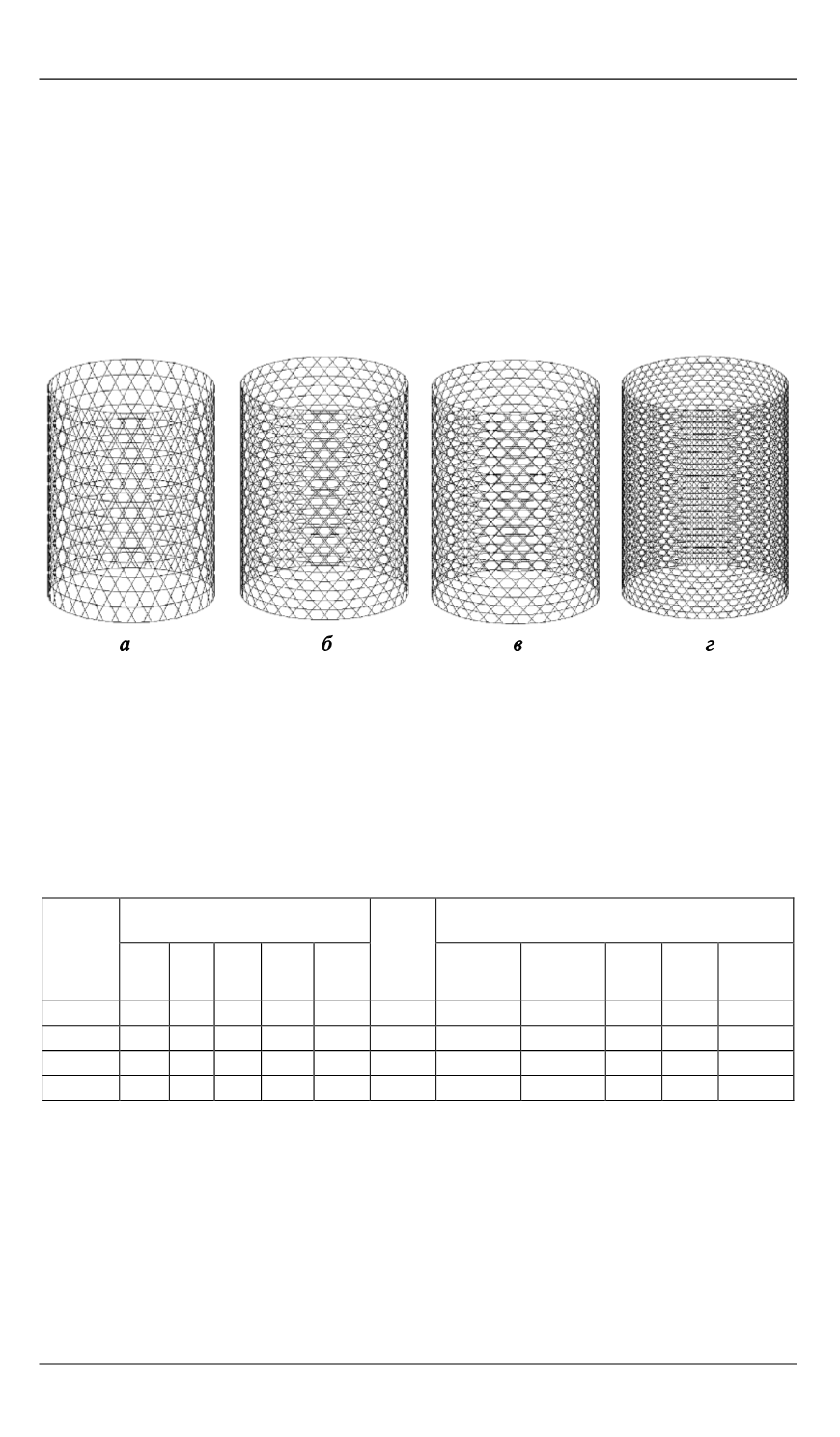
Рис. 4.
Топологическая структура сетчатых конструкций,
полученная в результате оптимизации:
а
— аналитические зависимости по выбору оптимальных параметров (
ϕ
= 24,5
°
,
m
h
= 32);
б
— циклический перебор по аналитическим зависимостям (
ϕ
= 36
°
,
m
h
= 32);
в
,
г
— симплексный поиск с ограничениями, представленными аналитическими
зависимостями (
ϕ
= 39
°
,
m
h
= 32;
ϕ
= 38,5
°
,
m
h
= 49)
Результаты оптимального проектирования
Номер
расчета
Оптимизационный расчет
Объем
V
, м
3
Расчет напряженно-деформированного
состояния модели
ϕ
h
m
h
,
мм
,
δ
h
мм
c
,
δ
мм
min
,
σ
кгс/мм
2
max
,
σ
кгс/мм
2
,
s
u
мм
,
n
u
мм
λ
1
24,5 32 21
6
3
429,9 –26,4
7,1
6
1,8 0,0122
2
36 32 14
4
1
665,9 –67,9
50,8
31 11,5 –0,017
3
39 32 4
8
3,5 130,9 –70,4
55,33 54,8 13,2 0,0122
4
38,5 49 4
5,5
3
177,8 –44,8
39,5
43,1 8,2 0,0111
Топологическая структура сетчатых моделей приведена на рис. 4.
В таблице представлены результаты оптимизационного расчета и
численных расчетов напряженно-деформированного состояния моде-
лей при осевом сжатии: максимальные значения напряжений в спи-
ральных
min
σ
и кольцевых
max
σ
ребрах и максимальные перемеще-
ния по образующей
s
u
и нормали
n
u
к поверхности, а также первые
собственные значения λ. Вычисления выполнены в пакете программ
















