
А.Ф. Киселев, В.В. Коваленко, Т.М. Притуло
4
Инженерный журнал: наука и инновации
# 8·2017
с применением двухшаговой конечно-разностной маршевой схемы
Мак-Кормака [5]. На гладких решениях эта схема имеет второй порядок
точности по всем координатам, и она является условно устойчивой с
числом Куранта, равным единице. Для построения разностной сетки
используются конформные преобразования Кармана — Треффтца [6].
При создании вычислительной программы [7] применены специальные
алгоритмы монотонизации, корректирующие решение в областях с
большими градиентами газодинамических параметров. Особый
расчет выполняется на поверхностях тела и выделенного головного
скачка. Последующий пересчет эволюции возмущенного течения при
распространении на большие расстояния выполняется с помощью
метода [8], основанного на квазилинейной теории [9]. Оказывается,
что на удалении от тела порядка 5–10 длин самолета трехмерное поле
течения вблизи самолета вырождается в независимое в каждой
азимутальной плоскости течение от некоторого эквивалентного тела
вращения.
Задача определения интенсивности звукового удара сводится к
решению системы обыкновенных дифференциальных уравнений
независимо в каждой азимутальной плоскости. Далее следует приме-
нить теорему профессора Ю.Л. Жилина [8], согласно которой эквива-
лентное тело вращения можно определить через ближнее поле около
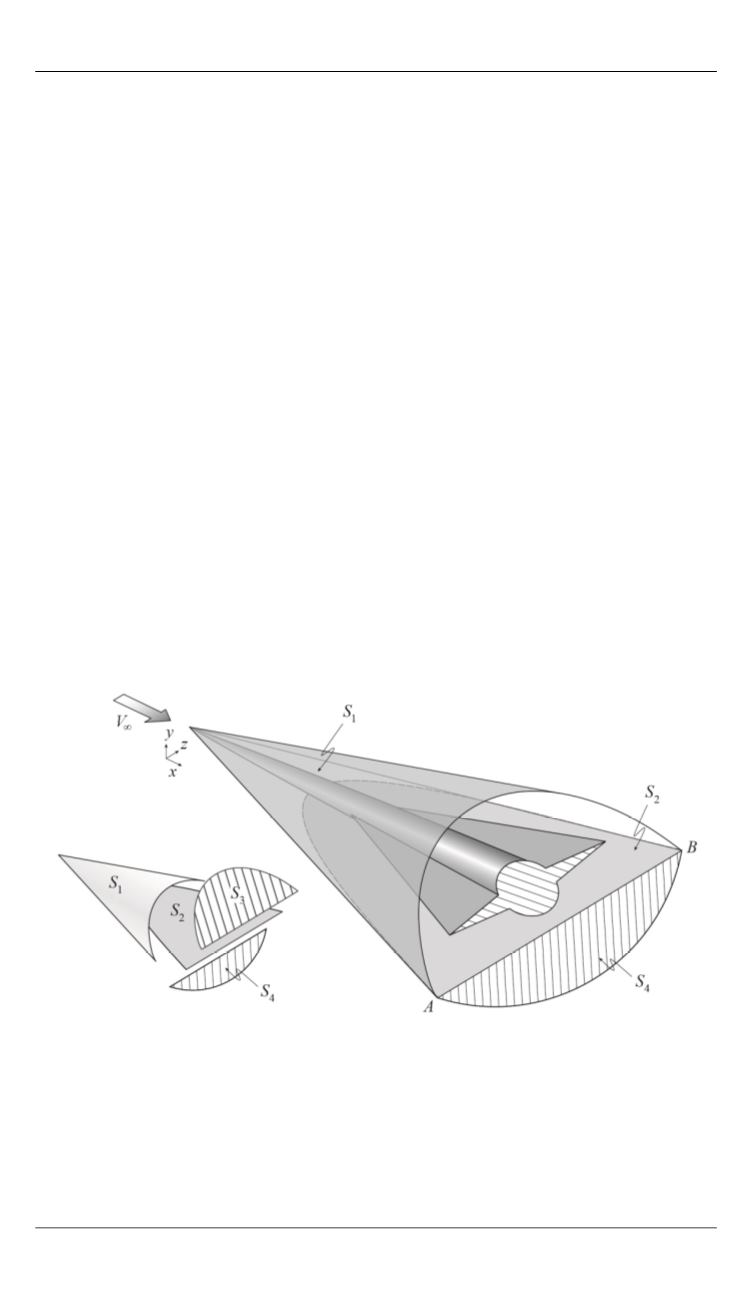
компоновки самолета (рис. 2).
Рис. 2.
Контрольный объем сверхзвукового обтекания компоновки самолета
Ю.Л. Жилин показал [8], что асимптотически удаленное реше-
ние, при некоторых допущениях, можно связать с интегралом в
ближнем поле на некоторой поверхности
S
2
, расположенной на уда-
лении от самолета около 0,1–0,5 его длины
L
. Если учесть, что воз-
















