
И.Б. Ставицкий, А.С. Шевченко
2
Инженерный журнал: наука и инновации
# 3·2017
обработки, для обработки титана и его сплавов применение метода
ограничено. Поэтому определение рациональных параметров им-
пульсов для обработки титана приобрело актуальность. Подчеркнем,
что получение эмпирических зависимостей связано с проведением
большого объема экспериментальных исследований, а значит, боль-
шими затратами времени и средств [1–5]. Кроме того, при получении
указанных зависимостей обычно не учитывают физические особен-
ности процесса электроэрозионной обработки. По эмпирическим за-
висимостям не всегда удается назначить оптимальные параметры им-
пульсов, которые бы обеспечивали максимально возможную произво-
дительность процесса формообразования. Поэтому в целях сокращения
объема экспериментальных исследований при разработке расчетных
зависимостей целесообразно проведение предварительного расчета на
основе рассмотрения тепловых процессов, происходящих при электро-
эрозионной обработке непосредственно в зоне воздействия электриче-
ского разряда.
Определение рациональных параметров
импульсов электроэрозионной обработки ти-
тана.
Оценить обрабатываемость материала
методом электроэрозионной обработки и вы-
брать рациональные импульсы для нее можно
путем решения задачи о перемещении границы
фазового превращения материала — так назы-
ваемой тепловой задачи Стефана [6], т. е. необ-
ходимо определить зависимость глубины про-
плавления материала от времени, исходя из
физических свойств материала, плотности теп-
лового потока
q
и длительности его действия
(рис. 1).
Задачу Стефана для двухфазной системы описывают системой
дифференциальных уравнений второго порядка, которые представ-
ляют собой основное уравнение теплопроводности для случая неста-
ционарной теплопроводности в полубесконечном твердом теле [6, 7]:
2
1
1
1 2
,
∂
∂ =
∂
∂
T
T а
t
x
0 <
x
<
η
;
(1)
2
2
2
2
2
,
∂
∂ =
∂
∂
T
T а
t
x
η
<
x
<
∞
,
где
ɑ
1,2
,
T
1,2
— соответственно температуропроводность и темпера-
тура жидкой (
1
) и твердой (
2
) фаз (см. рис. 1);
η
— координата гра-
ницы фазового превращения.
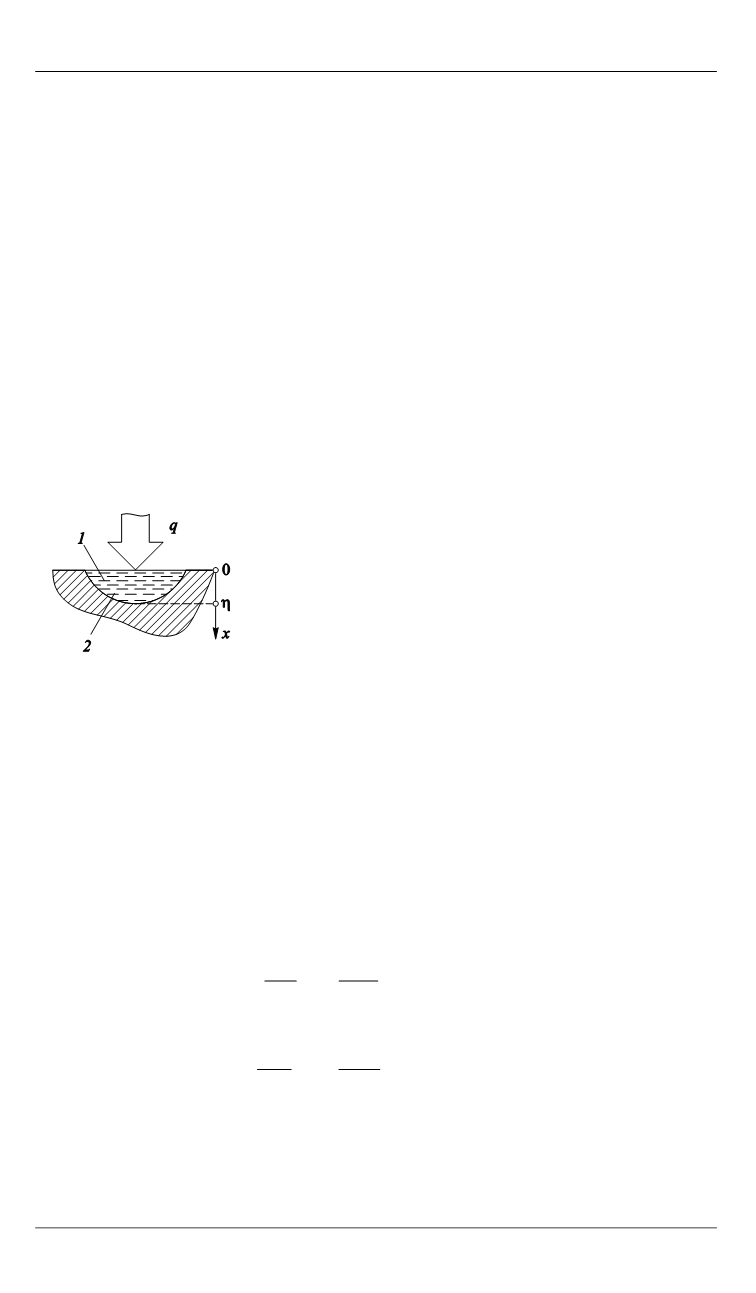
Рис. 1.
Схема для опре-
деления границы фазо-
вого превращения ма-
териала:
1
— жидкая фаза;
2
—
твердая фаза
















