
Б.Т. Добрица
,
Д.Б. Добрица
6
Инженерный журнал: наука и инновации
# 11·2016
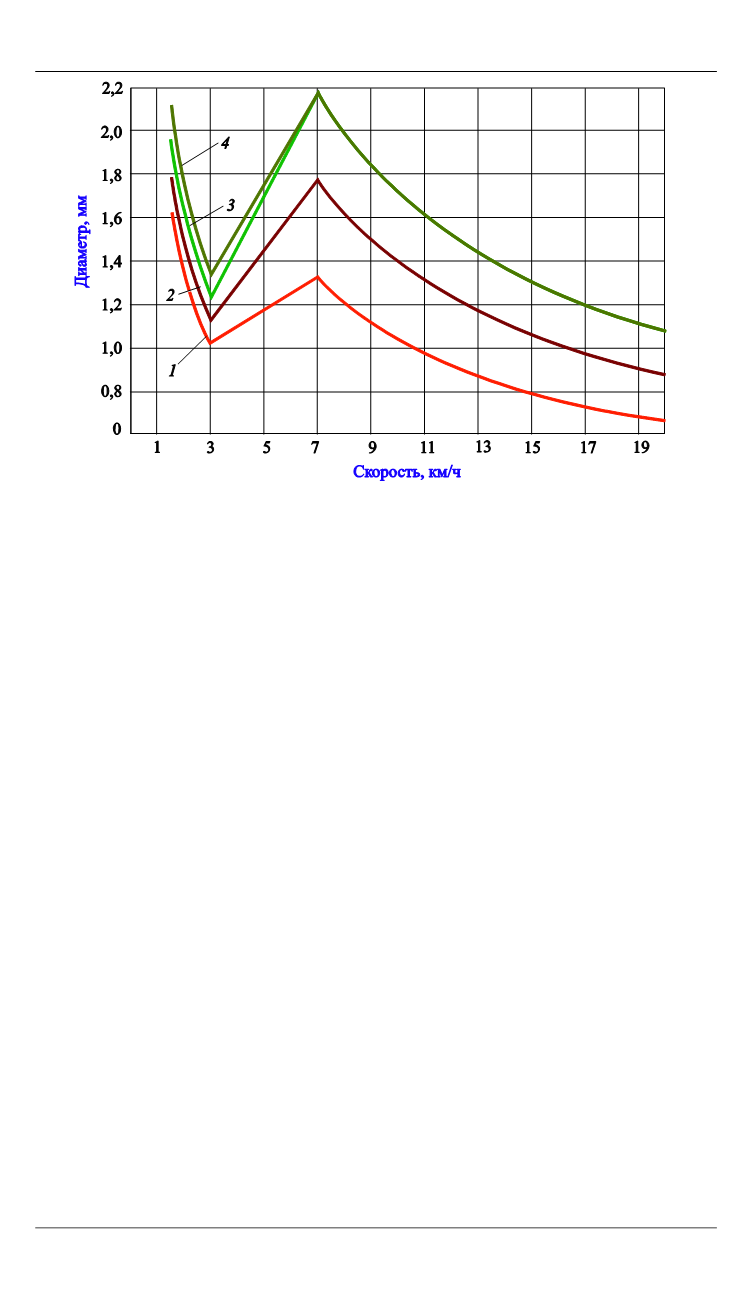
Рис. 2.
БПЗ конфигурации 1 при изменении толщины стенки бампера:
1–5
—
t
b
= 0,5; 0,6; 0,7; 0,8 и 0,9 мм соответственно
Конфигурация 2, характерная для расчетов стойкости элементов
КА к воздействию метеорно-техногенных частиц, имеет следующие
параметры:
t
b
= 1,5 мм,
t
w
= 1 мм,
S
= 4 мм, материал бампера и зад-
ней стенки — алюминиевый сплав АД31.
Для расчета БПЗ в конфигурации 2 определим по соотношению (8)
предельную толщину бампера. В данном случае рассматриваем
упрощенную конструкцию, которая сводится к двум стенкам с рас-
стоянием между ними
t
b
max
= 0,2 мм, что значительно меньше имею-
щейся толщины 1,5 мм. Очевидно, что при увеличении толщины
бампера расчет по формуле (2) для суммарной толщины бампер +
задняя стенка даст значение стойкости конструкции выше, чем рас-
чет по формуле (4) для двойной стенки на высокоэнтальпийном ин-
тервале скоростей. При произвольном увеличении толщины бампера
t
b
>>
t
w
БПЗ структуры будет стремиться к БПЗ одностенной кон-
струкции, толщина которой равна
t
b
+
t
w
. Очевидно также, что эффект
бампера должен проявляться плавно при увеличении расстояния
между стенками, начиная от нулевого. Если эффект бампера прояв-
ляется в расщеплении ударника на вторичное облако осколков, кото-
рые разлетаются в конический сноп [15], то площадь воздействия
вторичного облака на заднюю стенку (т. е. эффект рассеяния вторич-
ных осколков) будет увеличиваться пропорционально квадрату рас-
стояния между стенками.
Для расчета БПЗ двухстенных конструкций с относительно близ-
ким расстоянием между стенками уравнение Кристиансена и Керра
модифицировано с учетом этих соображений. Суть усовершенство-
















