
А.Г. Ребеко
14
Инженерный журнал: наука и инновации
# 5·2016
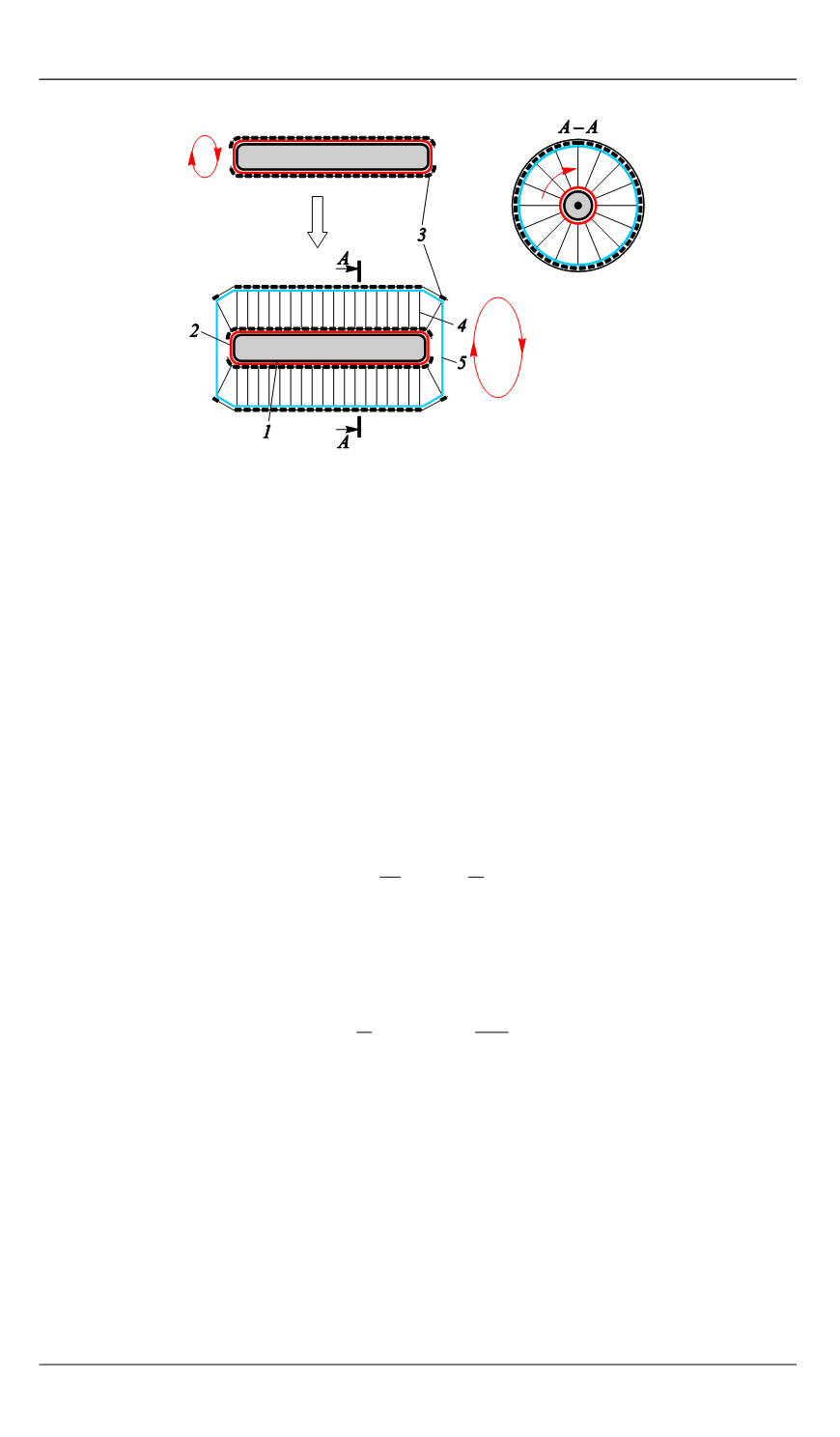
Рис. 10.
Зарядка цилиндрического конденсатора пере-
менной емкости при вращении:
1
— вращающийся цилиндр;
2
— изолятор;
3
— заряженный
сегмент;
4
— кварцевый трос;
5
— пленка внешней оболочки
Вначале в сложенном состоянии такой конденсатор заряжается
до относительно низкого напряжения (600 кВ при толщине изолятора
из плавленого кварца 1 мм). Затем цилиндр (обкладка) начинает
быстро вращаться, и в конце концов металлические сегменты отры-
ваются от цилиндра. При удалении такой импровизированной об-
кладки емкость конденсатора начинает уменьшаться.
При постоянстве заряда на обкладках разность потенциалов
U
между ними начинает расти, одновременно увеличивается и энергия ε
конденсатора, что выражено следующими формулами:
;
QU
C
=
2
1 =
,
2
CU
ε
где
Q
—
заряд;
C
—
емкость конденсатора.
Таким образом, кинетическая энергия «ротора» переходит в по-
тенциальную энергию конденсатора:
1 = ;
2
QU
ε
2
.
2
Q
С
ε =
Рассмотрим конкретный пример без обсуждения возможности
технической реализации. Предположим, что радиус внутренней об-
кладки
R
1
= 1,5 м, длина цилиндрического конденсатора
L
= 31 м,
расстояние между обкладками до раскрутки 1 мм, разность потенци-
алов между обкладками 600 кВ. Тогда до раскрытия емкость кон-
денсатора составит 2,6
⋅
10
–6
Ф, энергия электрического поля 470 кДж,
капсулированный заряд 1,55 Кл. Сила притяжения будет равна
9,3
⋅
10
8
Н, что составит давление 32 атм на поверхности обкладок.
Для отрыва заряженных сегментов от поверхности цилиндра сила


















