
Определение контактного давления для цилиндрических тел в задаче…
3
неподвижен, другой вращается относительно него с постоянной уг-
ловой скоростью
,
.
V
На торцах цилиндров имеются покрытия
толщинами
1
h t
и
2
.
h t
Ось
Oz
направим вдоль оси цилиндров. Так
называемый третий слой [1–5, 10, 11] толщиной
тоже имеет вид ци-
линдра.
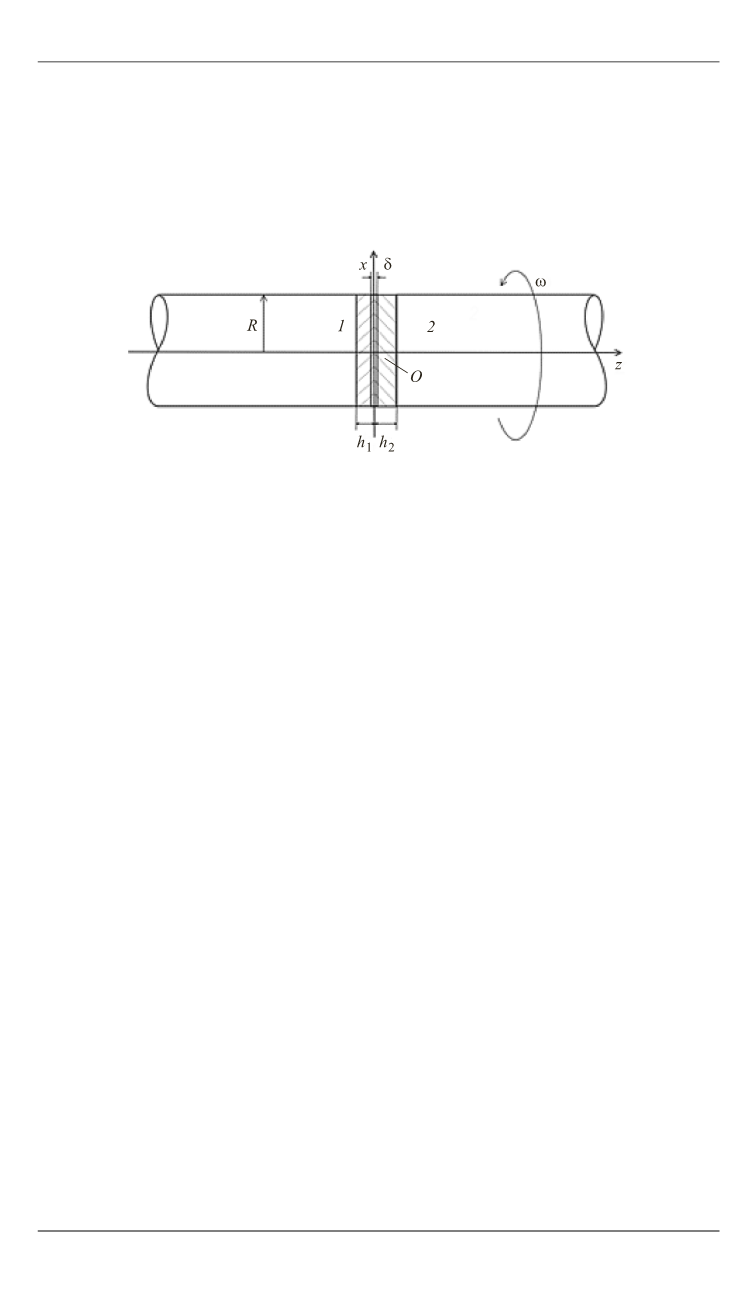
Схема контакта двух соосных цилиндров
Вследствие трения в области контакта возникает износ поверхно-
стей покрытий и изменение их толщин за счет износа и термоупругих
деформаций. Обозначим текущие значения толщин покрытий через
1
h t
и
2
.
h t
Износ будем считать абразивным, тогда уменьшение
толщин покрытий [13]
1*
1
1
2*
2
2
0
0
0
0
,
;
,
,
t
t
t
t
v t
l V d l V k q T d v t
l V d l V k q T d
(3)
где
1 2
,
l l
— коэффициенты износостойкости материалов покрытий.
Определение ресурса трибосопряжения.
Допустим сначала, что
функция
( )
q t
задана и найдем ресурс работы пары тел с покрытиями.
Очевидно, что должны выполняться равенства
1 1
1
10 1
*
,
;
v h t v t
h h t
2 2
2
20 2
*
,
,
v h t v t
h h t
(4)
где
,
i
v z t
— упругие перемещения точек покрытий по оси
z
;
*
i
v t
определяются формулами (3). Относительно
1 1
,
v h t
и
2 2
,
v h t
отметим, что с уменьшением
( )
i
h t
справедливы асимптотические со-
отношения
1 1
1
,
;
v h t O h
2 2
2
,
v h t O h
(5)
(следуют из формул (13), которые будут приведены далее).
Предположим, что износ достаточно развит, тогда в соответствии
с формулами (4) и (5) можно записать
















