
А.В. Бабкин, С.В. Ладов, С.В. Федоров
6
Для оценки характерных значений частоты разряда, при которых
реализуется эффективная диффузия внешнего магнитного поля в по-
лость оболочки, рассмотрим следующую задачу [18].
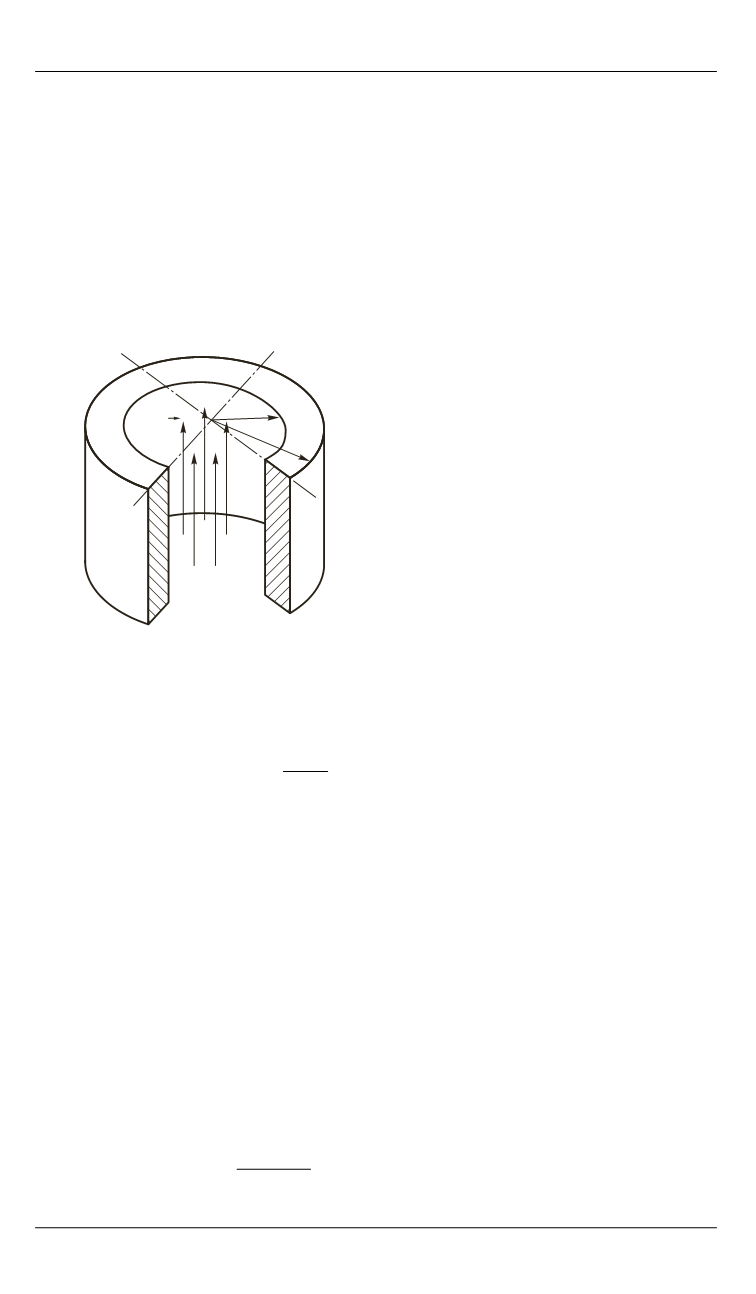
Проводящий цилиндр с внутренним
вн
a
и наружным
нар
b
радиу-
сами помещен во внешнее аксиальное нестационарное магнитное поле
(рис. 5). Следуя работе [18], зададимся постоянством объемной плот-
ности токов по толщине стенки цилиндра. Отметим, что такое предпо-
ложение в связи с интересующими нас достаточно медленными изме-
нениями внешнего поля в данном случае вполне обоснованно.
Рис. 5.
Расчетная схема проводящего
цилиндра в аксиальном нестационарном
магнитном поле
При указанном допущении уравнение диффузии магнитного поля
в полый цилиндр сводится к обыкновенному дифференциальному
уравнению
вн
вн
0
внеш
( ),
dB
B t
B
dt
(2)
где
0
— постоянная времени диффузии;
вн
B
— индукция магнитно-
го поля в полости цилиндра.
Постоянная времени диффузии
0 0 вн нар вн
/ 2.
(
)
b a
a
(3)
Удельную электрическую проводимость материала оболочки
в
формуле (3) при этом считают неизменной.
Полагая, что в начальный момент времени
0
t
магнитное поле в
полости цилиндра отсутствует
вн
(
0),
B
а внешнее магнитное поле из-
меняется по синусоидальному закону с частотой
:
внеш 0
sin ,
B B t
запишем решение уравнения (2) в следующем виде:
0
1
вн
/
2
0
2
0
0
sin
(
(
co .
)
s
1
B
B
t
e
t
t
(4)
b
нар
a
вн
B

















