
Н.В. Кирюхина, А.К. Горбунов, Н.А. Силаева
2
экв
4 ,
S
d
P
(1)
где
S
— площадь поперечного сечения;
P
— полный (смоченный) пе-
риметр канала.
Метод расчета теплоотдачи с помощью эквивалентного диаметра
является приближенным, точные границы применимости его не уста-
новлены [2]. Поэтому остается актуальной задача моделирования
гидродинамики и теплообмена в призматических каналах с учетом
геометрии поперечного сечения.
Целью данной работы является численное моделирование процес-
сов движения жидкости и теплоотдачи в каналах прямоугольного и
треугольного сечений. На первом этапе была решена задача о тепло-
обмене при развитом ламинарном течении в прямоугольном канале.
Считая канал бесконечно длинным, а плотность и коэффициент
вязкости постоянными, можно свести систему уравнений Навье‒
Стокса к уравнению Пуассона, которое в безразмерной форме при-
нимает вид
2
2
2
2
ω ω 1,
ξ η
(2)
где
ω
— безразмерная скорость;
ξ
и
η
— безразмерные координаты.
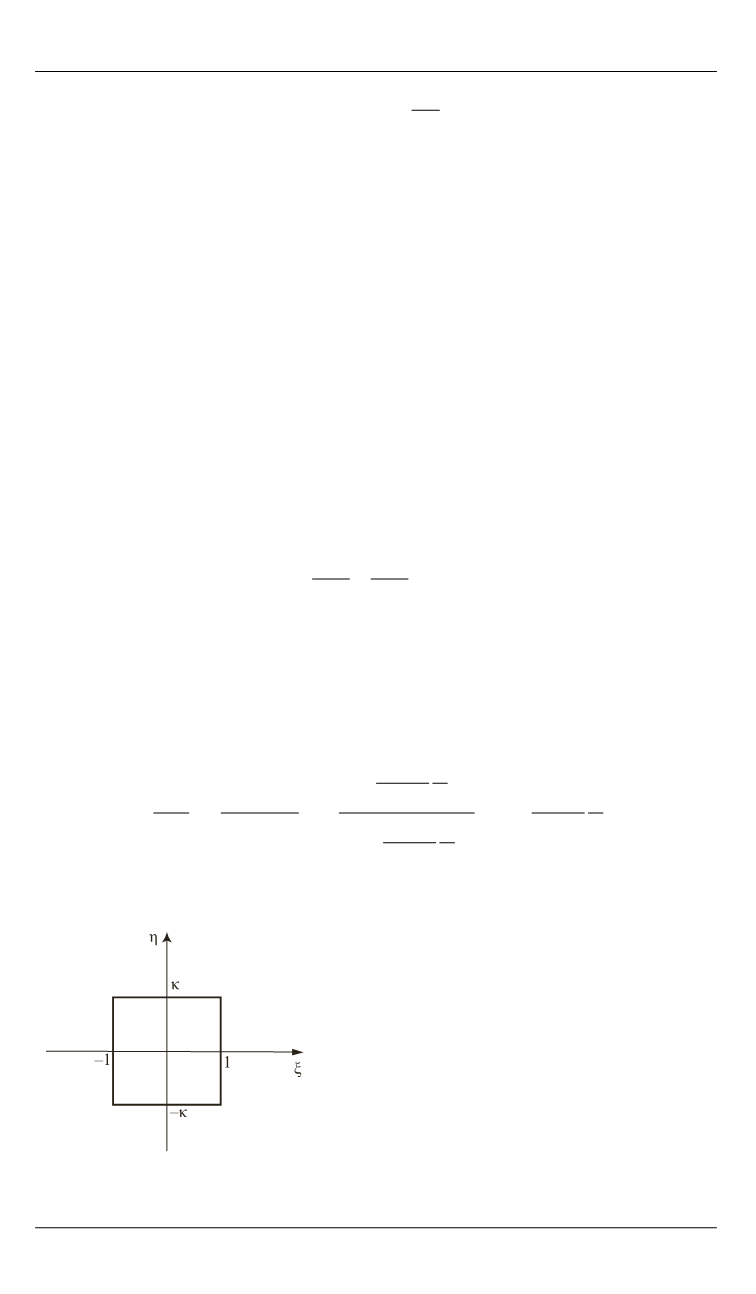
Для каналов прямоугольного сечения с отношением сторон
κ
(рис. 1)
это уравнение с граничным условием
ω
= 0 на стенках имеет анали-
тическое решение в виде ряда [3]:
3
3
0
2 1 π
ch
η
16κ ( 1)
2 1 π
2 κ
ω
1
cos
ξ .
2 1 π
2 κ
π (2 1)
ch
2 κ
n
n
n
n
n
n
(3)
Для канала треугольного сечения
(рис. 2) поле скоростей можно получить
аналитически, решая уравнение (2). Ес-
ли сечение представляет собой равно-
бедренный треугольник, боковые сто-
роны которого заданы уравнениями
η κ(1 ξ),
а основание
η 0,
то реше-
ние имеет вид
ω = η(η – κξ – κ)(η + κξ – κ),
(4)
где
κ
— отношение высоты к половине
основания.
Рис. 1.
Поперечное сечение
прямоугольного канала

















