Общие теоремы динамики и общее уравнение механики
3
так как внутренние силы образуют систему сил, эквивалентную ну-
лю, получаем выражение (4).
Теорема 2 (об изменении кинетического момента).
Если среди
виртуальных перемещений системы есть поворот системы как едино-
го целого вокруг оси
,
Oz
то
( , )
1
,
n
a e
z
z k
k
dK M F
dt
(5)
где
z
K
— кинетический момент системы при ее повороте вокруг оси
.
Oz
Доказательство.
Если виртуальным перемещением системы яв-
ляется поворот системы как единого целого вокруг оси
Oz
на угол
,
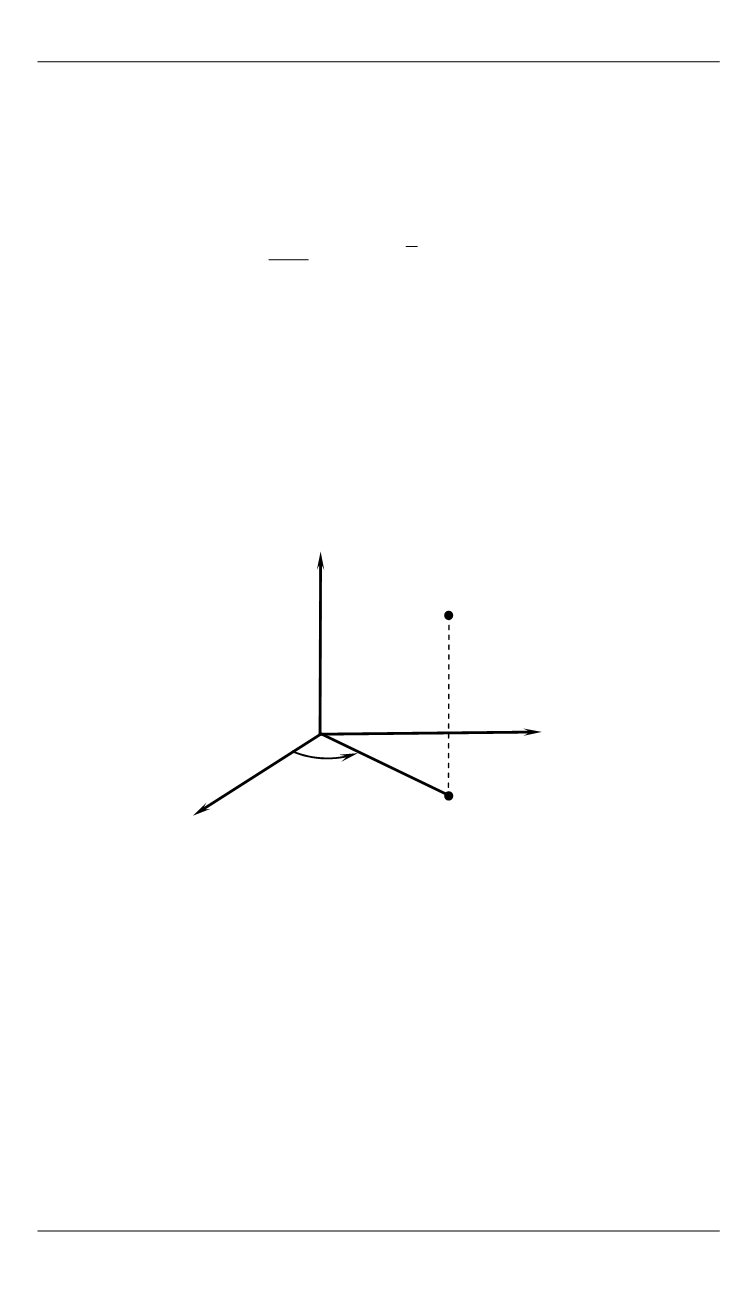
то декартовы и цилиндрические координаты
k
-й точки (см. рису-
нок) связаны соотношениями
cos ;
sin ;
.
k
k
k k
k
k k
k
x
y
z z
Декартовы и цилиндрические координаты точки
На рассматриваемом виртуальном перемещении
0;
0;
,
k
k
k
z
тогда
sin
;
cos
;
0.
k
k
k
k
k
k
k
k
k
x
y
y
x
z
Подставляя эти соотношения в общее уравнение механики (2),
получаем
( , )
( , )
( , )
( , )
1
0,
n
a e
a e
a i
a i
k k k
k k
k
k
k
k
ky
kx
ky
kx
k
m x y y x x F y F x F y F
тогда
y
z
O
x
k
k
) , , (
k k k k
z yxA


