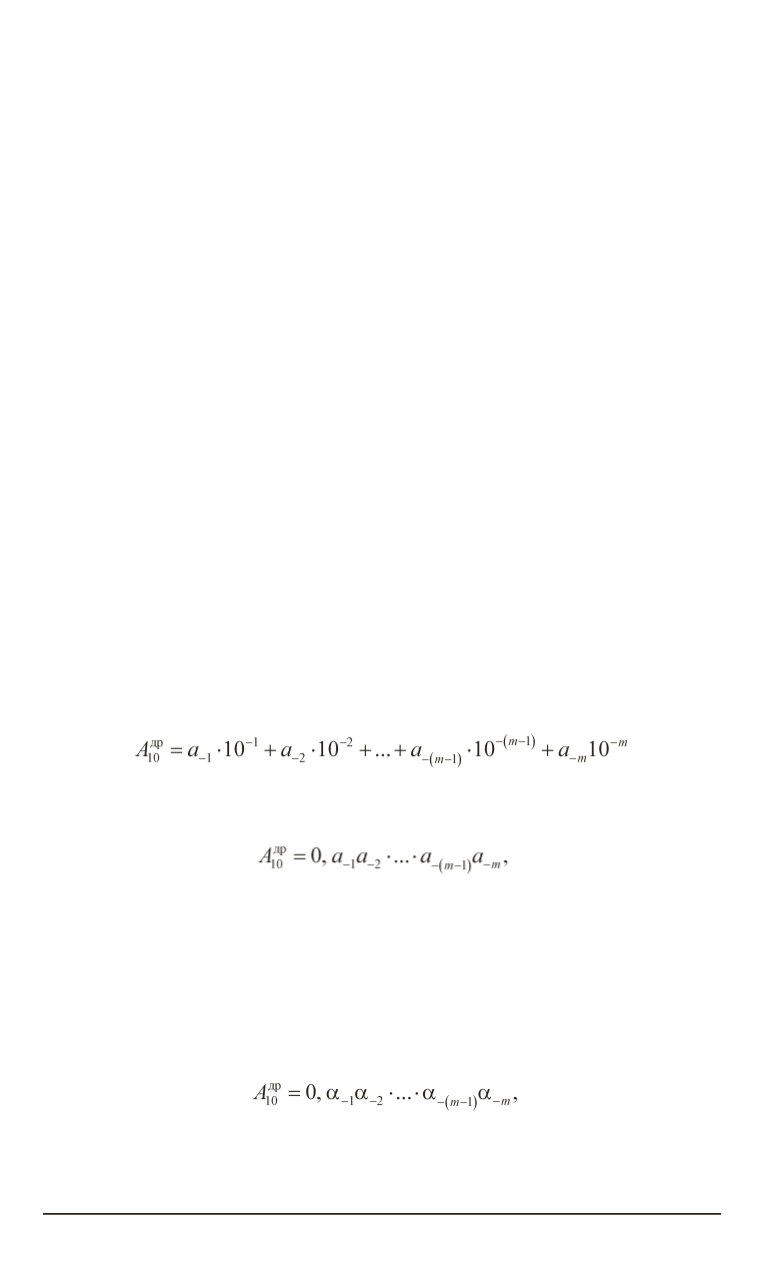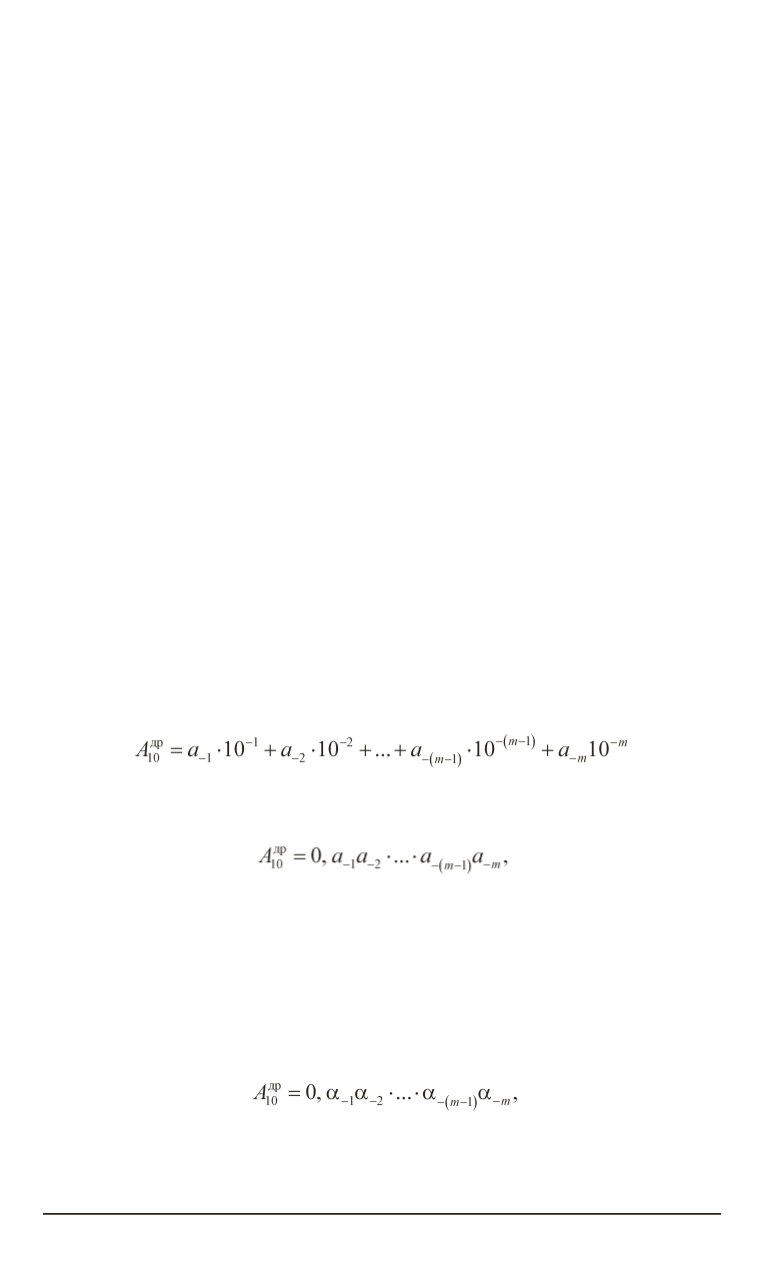
1
УДК 004.312.26
Преобразователь двоично-десятичного кода
правильных дробей в двоичный код
последовательностного типа
© В.Ф. Жирков, А.П. Калинин
МГТУ им. Н.Э. Баумана, Москва, 105005, Россия
Рассмотрен алгоритм преобразования двоично-десятичного кода правильных дро-
бей в двоичный код. Приведена реализация преобразователя многоразрядной дроби
последовательностного типа. Преобразователь такого типа, в отличие от комби-
национного, характеризуется однородностью построения схемы и, следовательно,
простотой наращивания разрядности преобразуемых чисел. Показано, что реализа-
ция преобразователя последовательностного типа на программируемых логических
интегральных схемах, например, фирмы Xilinx, позволяет выполнить преобразова-
ние 16-разрядной дроби за ~200 нс, 32-разрядной – за 400 нс при тактовой частоте
100 МГц.
Ключевые слова:
система счисления, двоично-десятичный код, двоичный код, преоб-
разователь, правильная дробь, ПЛИС, последовательностная схема.
Преобразование чисел из одной позиционной системы счисления в
другую выполняется в вычислительных устройствах и ЭВМ при вводе
и выводе данных отдельно для целой и дробной частей чисел.
Правильная десятичная дробь
A
др
записывается в виде
или в сокращенном виде при известном основании системы счисления
(1)
где
(
)
1 2
1
,
, ...,
,
m
m
a a a a
− −
−
− −
– цифры десятичной дроби (0, 1, …, 9);
1, 2, …,
m
– номера разрядов;
m
– число разрядов десятичной дроби,
знак «–» перед номерами разрядов указывает на то, что это разряды
дроби; 10 – основание десятичной системы счисления.
В двоично-десятичном коде (ДДК) 8421 дробь
A
др
имеет следую-
щее изображение:
(2)
где
(
)
1
2
1
,
, ...,
,
m
m
− −
−
− −
α α α α
– двоичные тетрады, равные 0000, 0001,…,
1001, изображающие десятичные цифры 0, 1,…, 9 соответственно.