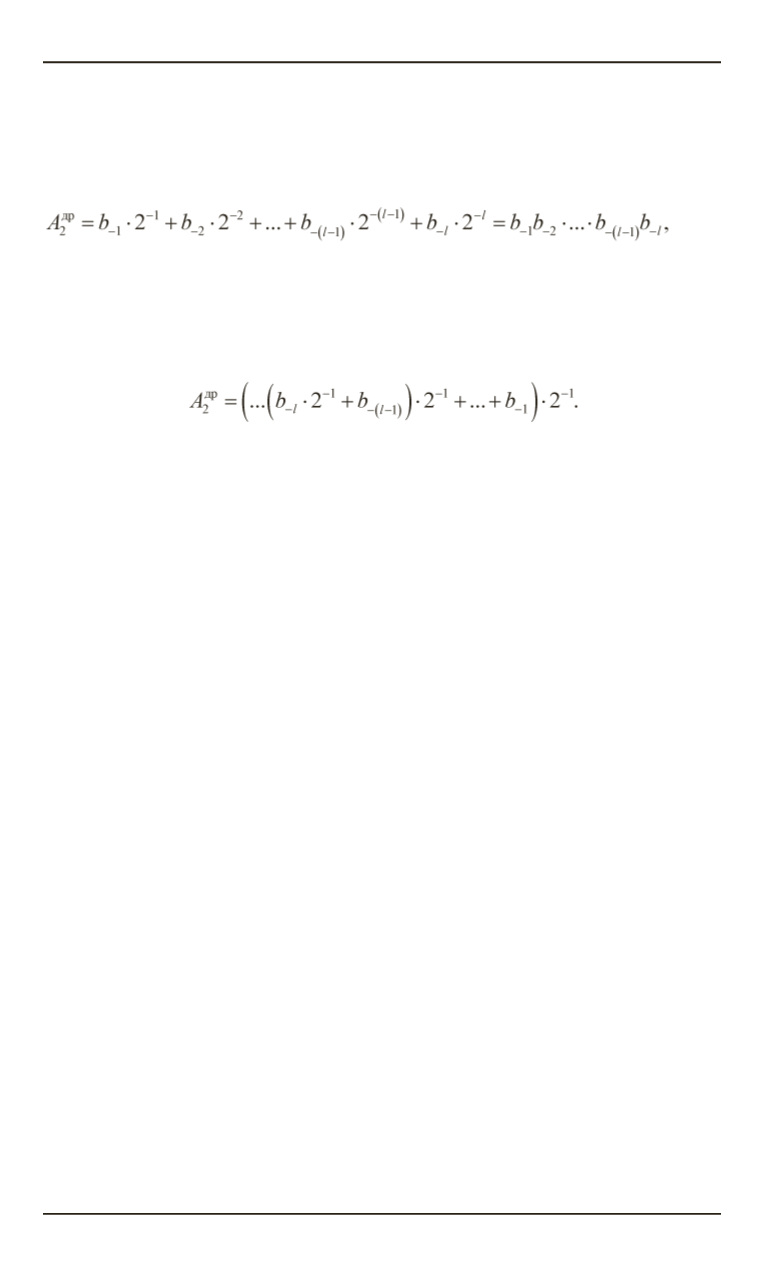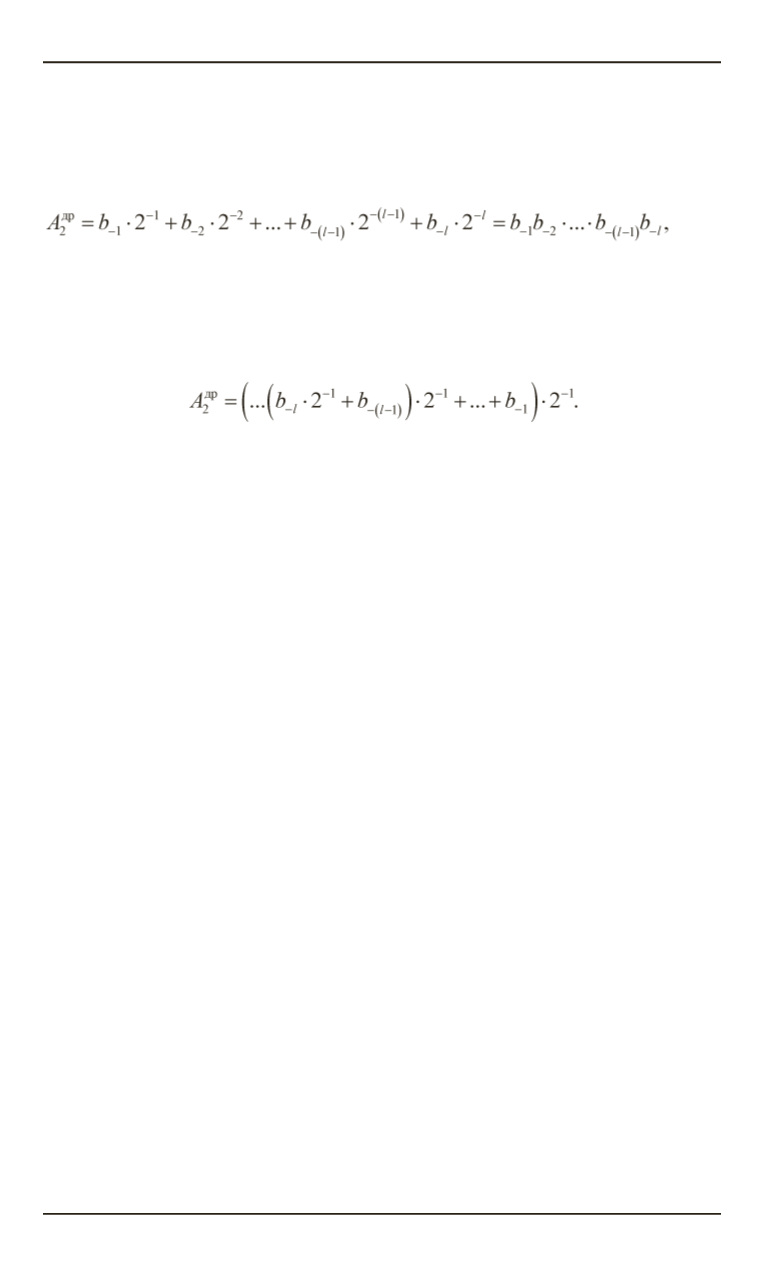
2
В.Ф. Жирков, А.П. Калинин
Тетрады 1010, 1011, 1100, 1101, 1110 и 1111 не используют и называют
псевдотетрадами. Цифры 8, 4, 2, 1 в обозначении кода – это веса раз-
рядов двоичной тетрады.
В двоичной системе счисления дробь
A
др
записывается в виде
(3)
где
( )
1 2
1
,
, ...,
,
l
l
b b b b
− −
−
− −
– цифры двоичной дроби, равные 0 или 1;
l
–
число разрядов двоичной дроби
др
2
A
.
Алгоритм преобразования правильной двоично-десятичной дроби
др
2 10
A
−
можно определить из записи выражения (3) по схеме Горнера:
(4)
Из выражения (4) следует, что для преобразования ДДК дроби
в двоичный код (ДК) необходимо последовательно умножать на 2
исходную дробь и дробные части получающихся произведений. При
каждом умножении получаются целые части, которые исключаются из
последующих операций умножения и представляют собой цифры дро-
би в двоичной системе счисления. Значение первой целой части явля-
ется старшей цифрой
b
–1
дроби. Умножив правую часть выражения (4)
на 2, получим неправильную дробь c целой частью
b
–1
, дробной –
( )
(
)
(
)
1
1
1
1
1
...
2
2 ...
2 .
l
l
b
b
b
−
−
−
−
−
− −
⋅
+ ⋅
+ + ⋅
Умножив полученную дробную
часть на 2, найдем новую неправильную дробь, целой частью которой
будет
b
–2
, дробной –
( )
(
)
(
)
1
1
1
3
1
...
2
2 ...
2 .
l
l
b
b
b
−
−
−
−
−
− −
⋅
+ ⋅
+ + ⋅
Повторяя процесс умножения
l
раз, определим все цифры
b
–1
,
b
–2
, …,
b
–
l
дроби в новой, т. е. двоичной, системе счисления. При этом
все действия выполняются в десятичной (исходной) системе счисления
над двоично-десятичными кодами дробей.
Умножение на 2 реализуется сдвигом ДДК дроби влево, т. е. в сто-
рону старших разрядов, на один двоичный разряд. Поэтому при сдвиге
цифры в тетрадах с весами 4, 2, 1 приобретают веса 8, 4, 2, иными сло-
вами, происходит умножение этих цифр на 2.
После каждого сдвига результат следует скорректировать, если
в результате сдвига возникает псевдотетрада или какая-либо единица
дроби переходит из одного двоично-десятичного разряда в другой.
В первом случае при значениях тетрад 5, 6 или 7 возникающие по-
сле сдвига псевдотетрады 1010, 1011,…, 1111 должны корректировать-
ся увеличением их на 6
10
= 0110
2
с передачей единицы переноса в сле-
дующую старшую тетраду. Во втором случае, если значение тетрады
до сдвига равно 8 или 9, единица при переходе в данный двоично-де-