И.К. Белова
6
для решения уравнения Пуассона или Лапласа данная опция не-
пригодна (вместо нее следует использовать встроенные функции
multigrid или relax);
в качестве метода решения используется метод прямых;
для решения систем дифференциальных уравнений в частных
производных следует использовать опцию numol.
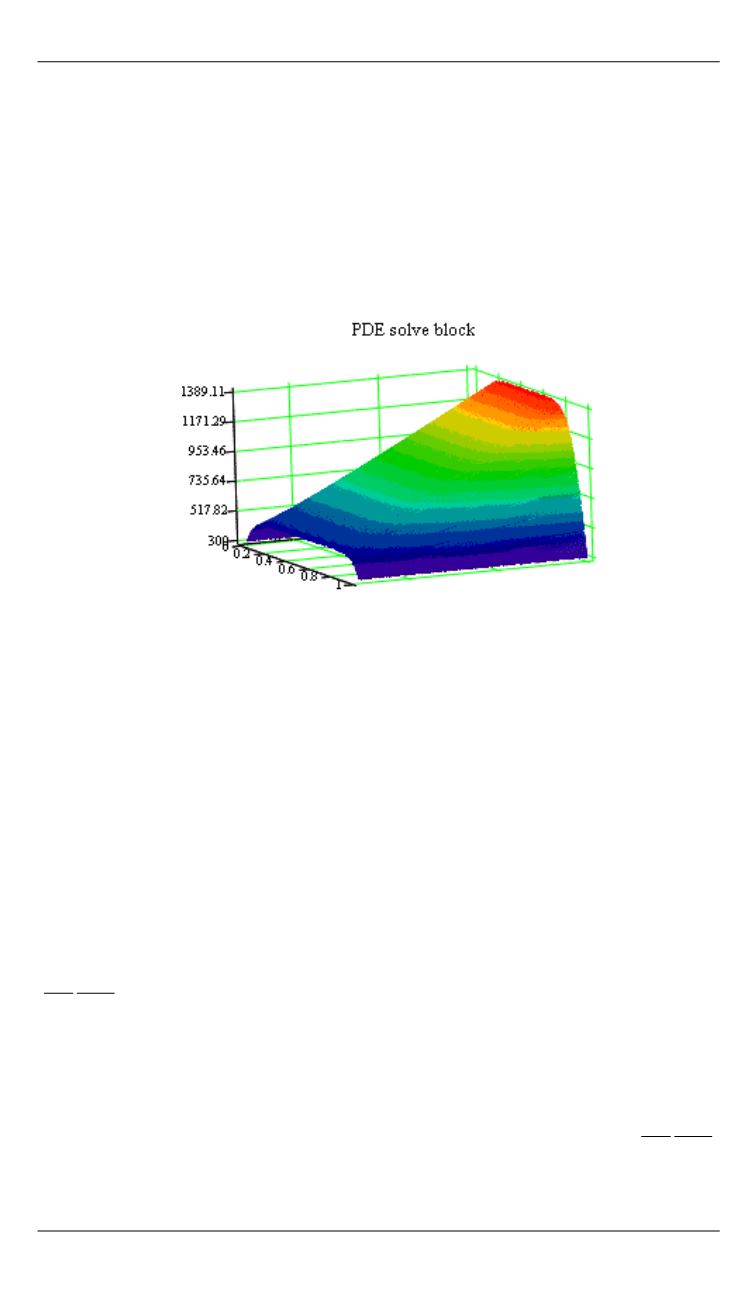
Для построения трехмерного графика решения имеется опция
CreateMesh , 0, , 0, ,
,
l
t
u L T N N
(рисунок).
График процесса разогрева идеального катода,
построенный средствами MathCad
Средства вычислительной техники позволяют рассматривать
обыкновенные дифференциальные уравнения, а не уравнения в част-
ных производных. Математическое различие между двумя классами
уравнений заключается в том, что для существования единственно-
сти решения обыкновенных уравнений достаточно лишь начального
условия, а условия на границах не рассматриваются. Это означает,
что обыкновенные дифференциальные уравнения не учитывают теп-
ловых потоков в теле катода, определяемых второй производной
температуры катода по координате. Уравнение (4) является обыкно-
венным дифференциальным уравнением в частных производных в
случае пренебрежения тепловыми потоками в теле катода (член
2
2
),
S
T
С x
что, строго говоря, возможно лишь в случае идеальных ка-
тодов прямого накала.
Математические требования необходимости граничных условий
при решении уравнений в частных производных имеют четкий физи-
ческий смысл: уравнение теплопроводности с членом вида
2
2
T
С x
учитывает тепловые потери в теле катода, существование которых


