И.Н. Овчаренко
4
Общее решение уравнения (2) при условии, что
0
,
имеет вид
1
cos(
),
t
x Ae
t
где
1
— частота затухающих колебаний,
2 2
1
0
.
Амплитуду и начальную фазу колебаний вычисляютпо формулам
0
0
0 1 1
,
arctg
.
cos
x
v
A
x
При большом коэффициенте затухания
0
(
)
движение имеет
непериодический характер, т.е. колебания не возникают и колеба-
тельная система возвращается в положение равновесия, не совершая
колебаний. Эта ситуация в данной работе не рассматривается.
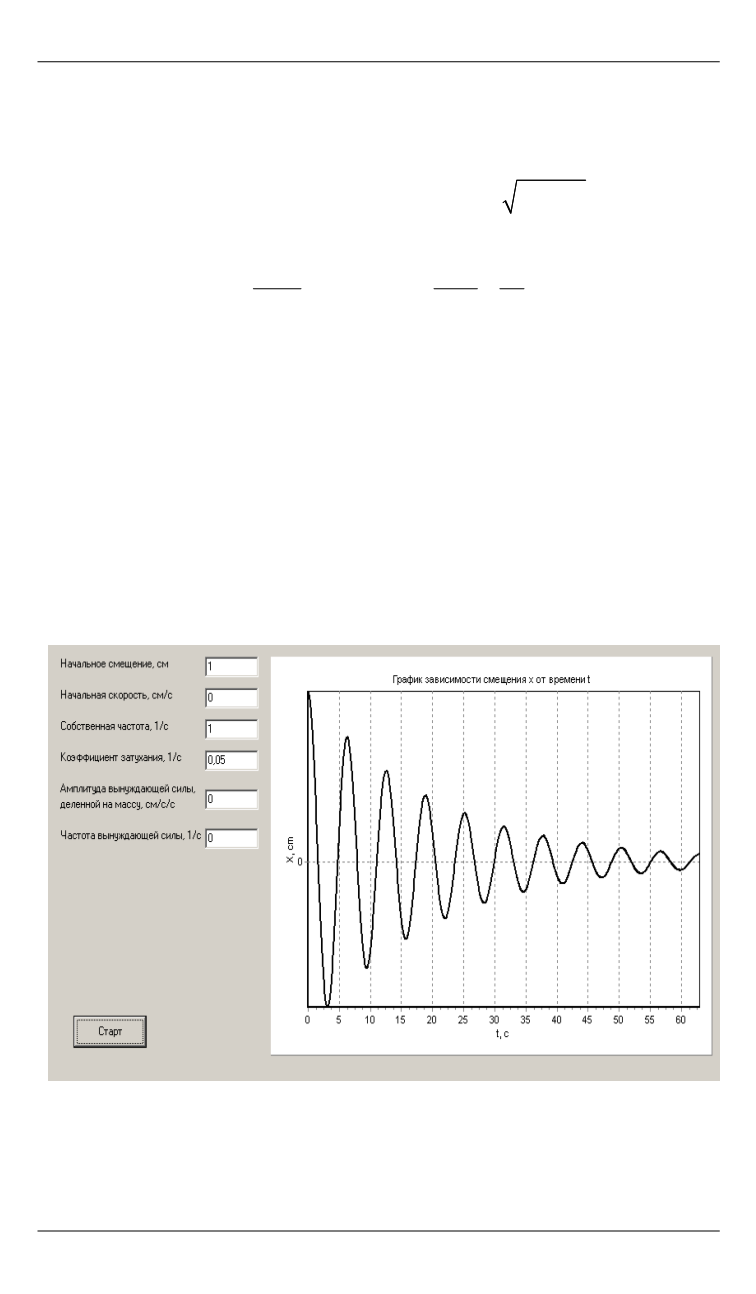
Перед запуском программы на счет для затухающих колебаний
необходимо указать начальные смещение и скорость, собственную
частоту колебаний и коэффициент затухания (остальные параметры
равны нулю). После запуска программа строит график зависимости
смещения от времени, полностью описывающий процесс затухаю-
щих колебаний (рис. 2). При этом отчетливо видна экспоненциальная
зависимость амплитуды колебаний от времени.
Рис. 2.
Процесс затухающих колебаний при малом коэффициенте затухания
Вынужденными являются колебания, протекающие в системе под
влиянием внешнего периодического воздействия [4, 5]. Такие коле-


