Моделирование взаимодействия цилиндрических и сферических тел с покрытиями …
5
В результате для максимальной (локализованной вблизи внешней
окружности оснований цилиндров) контактной температуры
*
T
с
учетом формулы (1) получим выражение
1
1 2
*
*
*
2
2 1 1 2
1 2
1 2 *
*
exp
,
1
exp
2
k q
h h R
T
k q
h h h h R
(7)
идентичное выражению для плоских поверхностей [2].
Определение максимальной контактной температуры в случае
трения сферических поверхностей.
Пусть в твердом теле имеется
сферическая полость с нанесенным покры-
тием толщиной
1
,
h
внутри которого нахо-
дится подвижный шар с покрытием толщи-
ной
2
.
h
Радиус сферической поверхности
контакта двух тел равен
.
R
Шар закреплен
на стержне, проходящем через его центр, и
вращается с постоянной угловой скоростью
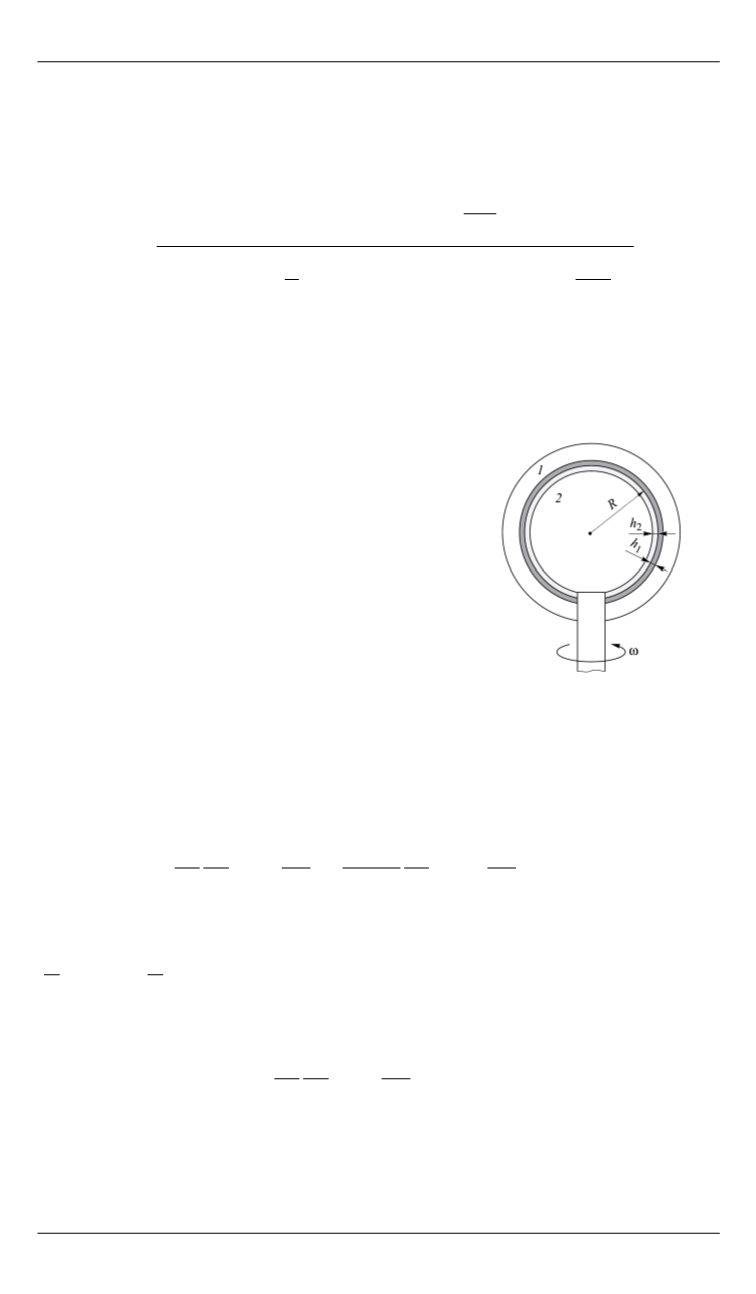
(рис. 2). Найдем максимальное значение
контактной температуры. Очевидно, что
оно достигается в точках с максимальной
линейной скоростью движения, т. е. в эква-
ториальной плоскости.
Перейдем в сферическую систему ко-
ординат. Температура не зависит от угла
,
поэтому уравнение теплопроводности для третьего слоя имеет вид
2
2
1
1
sin
.
sin
T
T f
(8)
Если рассматривать малый участок шарового слоя при
,
2
2
можно принять допущение, что температура не за-
висит от угла
и уравнение (8) принимает вид
2
2
1
.
T f
(9)
Граничные условия задачи теплопроводности между покрытия-
ми
1
и
2
(см. рис. 2) для неоднородного по теплофизическим свой-
Рис. 2.
Схема взаимодей-
ствия двух сферических
тел


