Метод расчета апланатической сферической линзы…
3
ванием в качестве исходных решение однородной линзы, удовлетво-
ряющее условию минимума сферической аберрации третьего поряд-
ка, и решения с близким к нему состоянием коррекции. В последних
сферическая аберрация несколько превышает достигаемое мини-
мальное значение. В [2] было показано, что п
ри переходе от линзы с
постоянным значением ПП к градиентной линзе с устраненной сфе-
рической аберрацией путем введения ОЛРПП в пределах стрелки
прогиба первой поверхности линзы или осевой толщины линзы вто-
рая сумма Зейделя градиентной линзы принимает значения, близкие
к значениям этой суммы в исходной линзе с постоянным значением
ПП при расположении входного зрачка в ее плоскости. После устра-
нения в линзе сферической аберрации путем введения градиентного
слоя вторая сумма Зейделя перестает зависеть от положения входно-
го зрачка.
На рис. 2, 3 представлены зависимости от радиуса кривизны пер-
вой поверхности линзы второй суммы Зейделя для однородной линзы
ܵ ̅
୍୍од
ݎ(
ଵ
)
и для исправленных в отношении сферической аберрации
неоднородных линз
ܵ ̅
୍୍нод
ݎ(
ଵ
).
Зависимости приведены для двух по-
ложений входного зрачка, а именно: при расположении входного
зрачка в плоскости, касательной к первой поверхности линзы (
s
p
= 0),
и при вынесении входного зрачка в пространство предметов на рас-
стояние
s
p
= –15 мм. Отрезок
s
p
определяет расстояние от вершины
первой поверхности линзы до центра входного зрачка. В линзах
ОЛРПП обеспечивается в пределах стрелки прогиба первой поверх-
ности (см. рис. 2) или на всей толщине линзы (см. рис. 3).
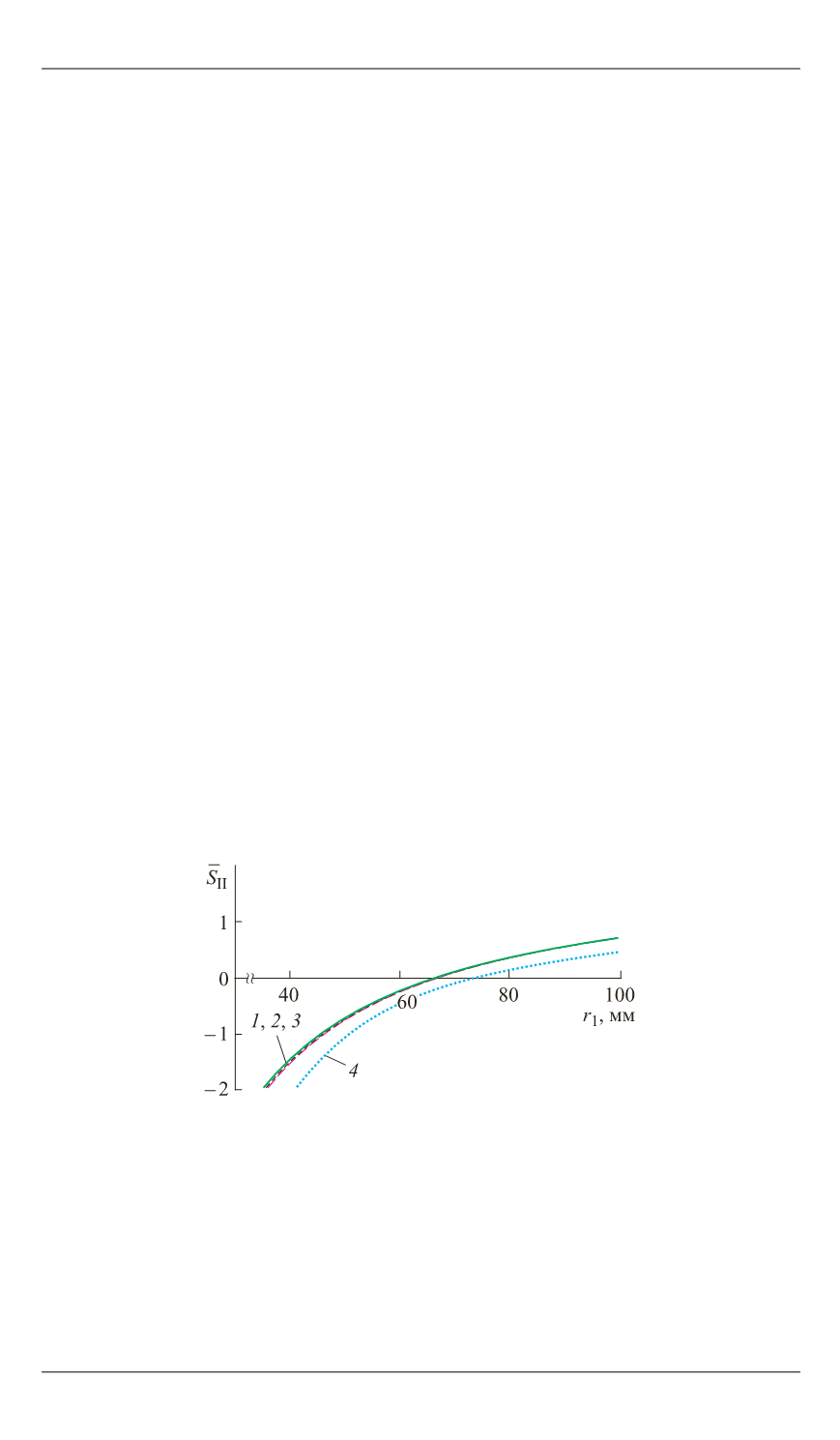
Рис. 2.
Первая
и вторая суммы Зейделя однородной
сферической линзы и исправленной в отношении
сферической аберрации градиентной линзы с
ОЛРПП в пределах стрелки прогиба первой поверх-
ности для дальнего предмета:
1
–
ܵ ̅
୍୍од
ݎ(
ଵ
)
для однородной линзы при
s
p
= 0;
2
–
ܵ ̅
୍୍нод
ݎ(
ଵ
)
для
неоднородной линзы при
s
p
= 0;
3
–
ܵ ̅
୍୍нод
ݎ(
ଵ
)
для неоднородной
линзы при
s
p
= – 15 мм;
4
–
ܵ ̅
୍୍од
ݎ(
ଵ
)
для однородной линзы при
s
p
= – 15 мм


