Т.С. Ровенская, А.Е. Алимов, К.Э. Квиткина
2
толщинами, определяемыми из конструктивных соображений. Так, в
«тонком» оптическом элементе его толщина
d
т.э
и заднее фокусное
расстояние
f '
связаны условием:
݀
т.э
≤ 0,1݂
ᇱ
[3]
. Аберрация кома рас-
сматриваемой линзы зависит от ее формы и положения входного зрач-
ка. При совмещении входного зрачка с линзой (соответствует совме-
щению плоскостей входного зрачка и плоскости, касательной к первой
поверхности линзы в ее вершине) изменение формы линзы при сохра-
нении ее фокусного расстояния сопровождается изменением знака ха-
рактеристического коэффициента третьего порядка комы (второй
суммы Зейделя
S
II
) с принятием суммой
S
II
нулевого значения при
конкретной форме линзы. За параметр, определяющий форму линзы,
принято значение радиуса
r
1
кривизны первой поверхности. При этом
нулевое значение второй суммы Зейделя определяется в области зна-
чений параметра формы линзы, близких к значению, при котором
находится минимум сферической аберрации [3].
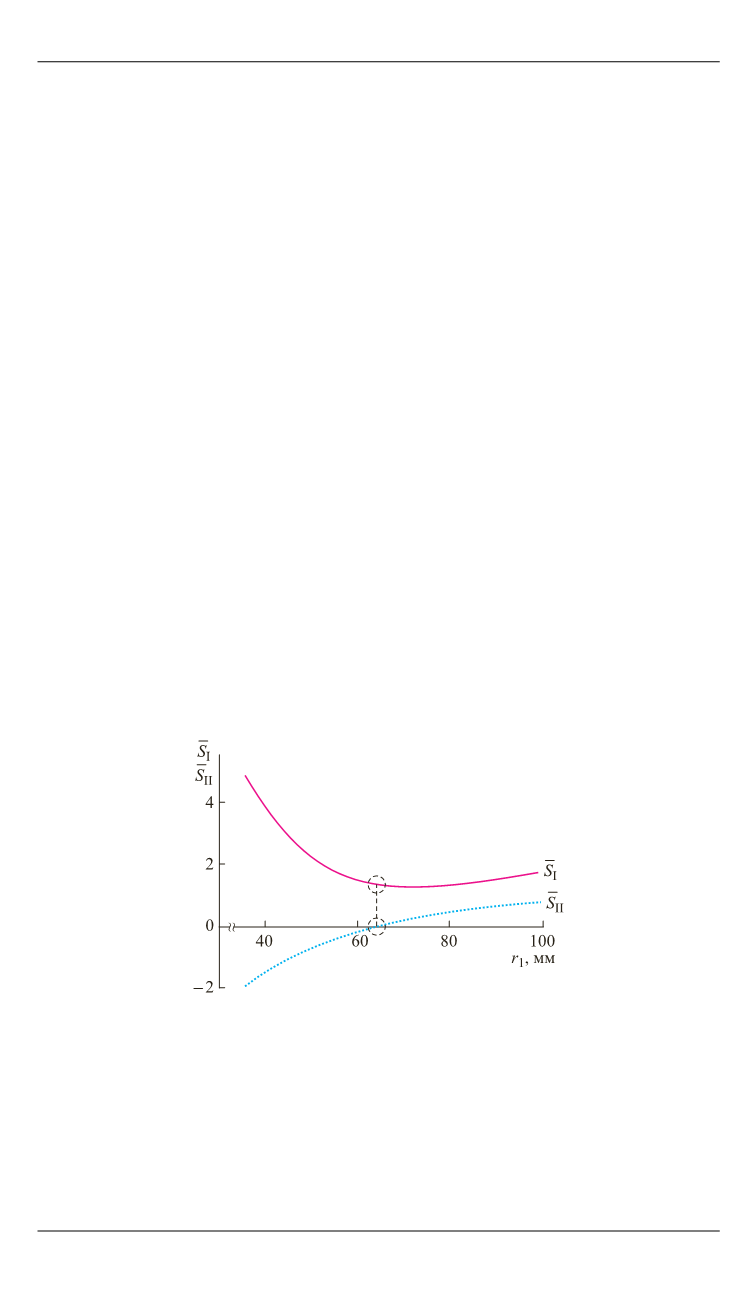
На рис. 1 представлены зависимости первой
S
I
и второй
S
II
сумм
Зейделя однородной сферической линзы от параметра формы линзы
r
1
при расположении предмета относительно линзы в бесконечности и
совмещении входного зрачка с линзой. Значения сумм Зейделя опре-
делены при канонической форме соответствующих им выражений [3].
Конструктивные
параметры сферических однородных линз получены
при заднем фокусном расстоянии
f '
=100 мм и осевой толщине
d
= 10 мм для ПП материала линз
n
= 1,7, при допущении, что радиус
кривизны первой поверхности является свободным параметром.
Рис. 1.
Первая и вторая суммы Зейделя однородной сфе-
рической линзы при дальнем предмете и входном зрачке
в плоскости линзы.
В [2] конструктивные параметры исправленных в отношении
сферической аберрации градиентных линз были получены при ука-
занных значениях фокусного расстояния и осевой толщины для отно-
сительного отверстия
D
/
f '
=1:2 и углового поля 2ω
= 30º с использо-


