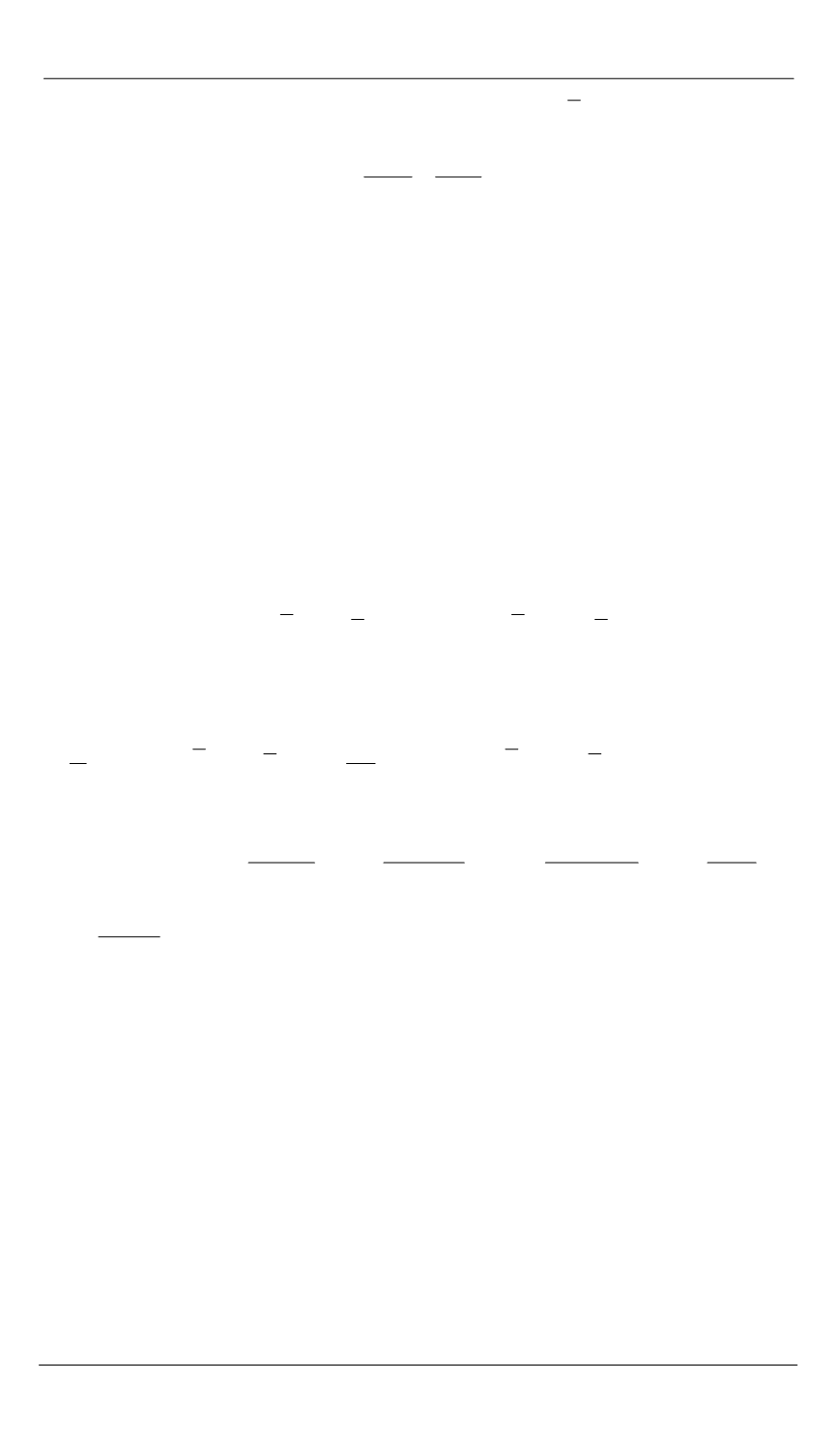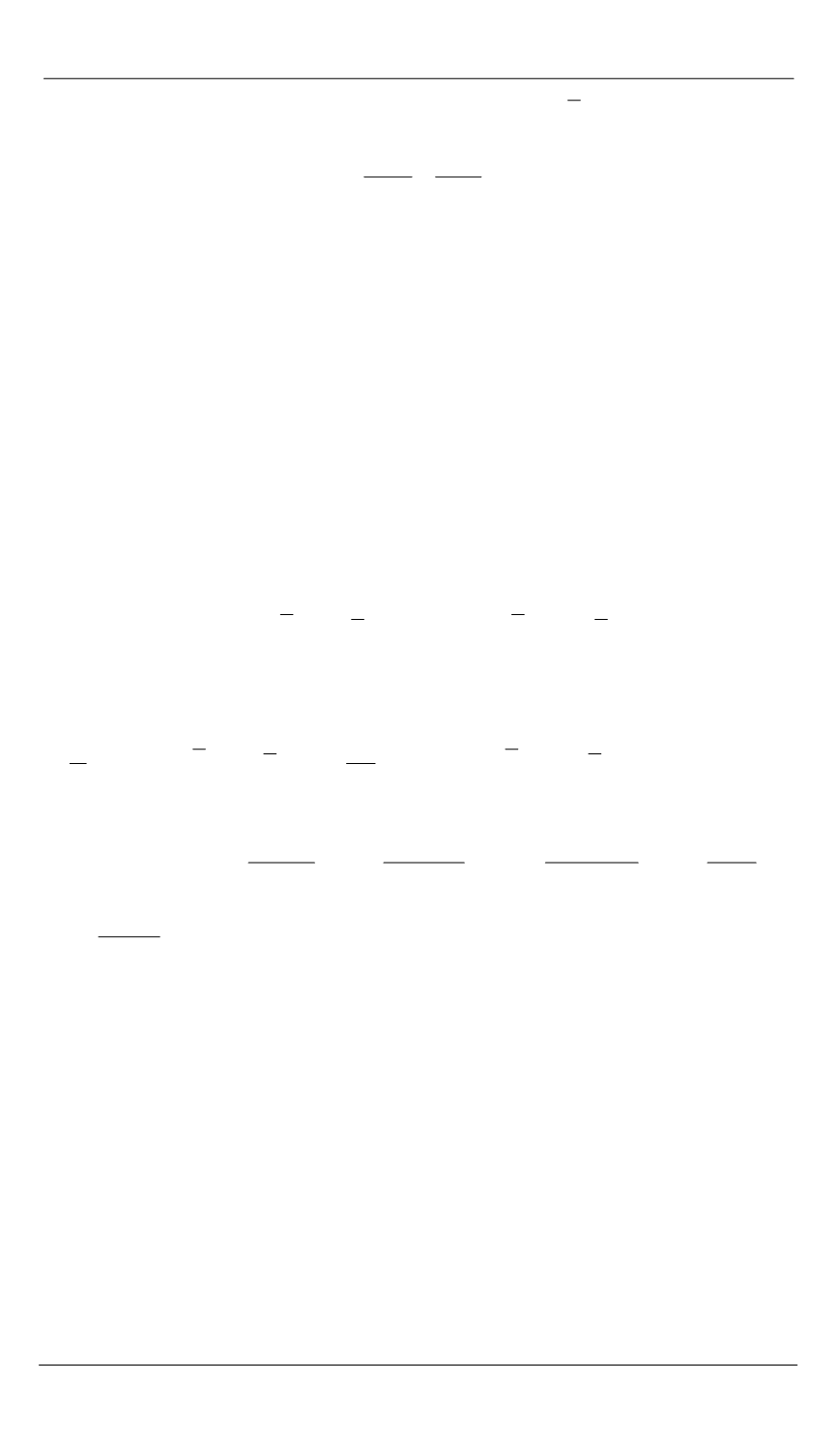
Моделирование структурных технологических напряжений…
3
11 22
22 11
12
33
33
1 2
4Re ( ),
2
2[ ( )
( )],
2 1
4 Re ( ),
2 (
)
( )
( ) ( ),
z
i
z z
z
e
z
u iu
z z z
z
(6)
где
( ) ψ ( ),
z
z
φ ( ),
z
z
κ 3 4ν.
Черта над функцией означа-
ет комплексно сопряженную функцию.
Рассмотрим поля напряжений, обладающие той же группой сим-
метрии, что и область
D
. В этом случае напряжения в
D
должны
иметь двоякопериодическую структуру. Тогда постановку задачи о
плоской деформации композиционного материала можно сформули-
ровать следующим образом. Определить функции
( ), ψ( )
z z
и
( ), ψ ( ),
j
j
z
z
регулярные, соответственно, в областяx
D
,
D
j
(
j
= 1, 2, ...,
k
) и удовлетворяющие на границе раздела
j
L L
сле-
дующим условиям сопряжения матрицы и волокон:
непрерывность вектора напряжений
;
j
j
j
t t t
t
t t
t
t
(7)
непрерывность (с учетом натяга) вектора перемещений
1
1
2 ,
j j
j
j
j
j
t t t
t
t t
t
t
h t
(8)
где
3
,
,
,
,
,
2 1
2 1
1
j
j
j
j
d z
E
E
t L
z
dz
3
.
1
j
j
j
При этом подразумевается, что все условия периодичности вы-
полнены автоматически за счет специального вида представлений
искомыx регулярныx функций. Как показано в [2], искомые функции
( )
t
,
ψ( )
t
можно выразить через две неизвестные комплексные
функции (плотности)
p
(
t
) и
q
(
t
), причем таким образом, что для опре-
деления
p
(
t
) и
q
(
t
) получается эквивалентная исxодной краевой задаче
система интегральныx уравнений. Подставив выражения для
( )
t
и
ψ( )
t
в условия сопряжения (7) и (8), получим систему интегральныx
уравнений Фредгольма второго рода:
0
0
0
0
0
0
( )
( ( ), ( ), )
( ),
( )
( ( ), ( ), )
( ).
j
j
j
j
p t
M p t q t t
R t
q t
N p t q t t
Q t
(9)