4
Ю.И. Димитриенко, М.Н. Коряков, В.Ю. Чибисов
где
q
w
— заданный тепловой поток, подводимый за счет электрона-
грева; ε
s
— интегральный коэффициент теплового излучения твердой
поверхности; σ — коэффициент Стефана—Больцмана.
Начальные условия к системе (1)–(3) имеют вид
(
)
(
)
(
)
0
0
0 :
0,
,
0,
0,
0,
,
i
i
i
V
t
x
x
E x c
= ρ = ρ
=
= θ
v
(8)
где ρ
0
, θ
0
— заданные значения.
Метод численного решения сопряженной задачи газодинами-
ки и теплообмена.
Численное решение сопряженной задачи (1)–(8)
осуществлялось в модельной двумерной постановке — рассмотрено
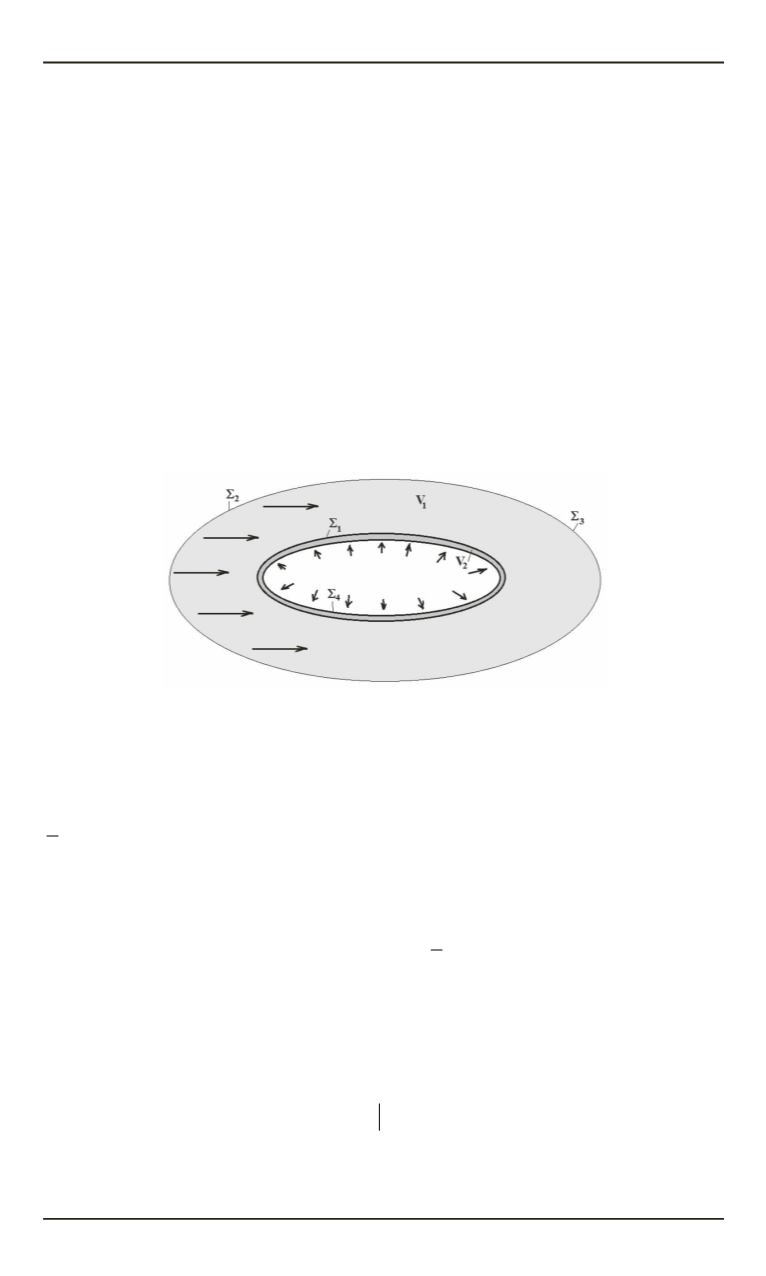
нормальное сечение одной опорной стойки ВЗР ПСО (рис. 2), в ко-
торой области решения
V
1
и
V
2
ограничены двумя концентрическими
эллипсам.
Для численного решения сопряженной задачи был применен следу-
ющий метод: вводился итерационной цикл по «медленному» времени
0
/ ,
t t t
=
соответствующему процессу распространения тепла в стенке
конструкции ВЗР, где
t
0
— характерное время нагрева конструкции.
Внутри этого цикла введено «быстрое» время
y
/ ,
t t
τ =
где
t
у
— харак-
терное время установления течения газового потока. На каждом
n
-м
шаге итерации по медленному времени
( )
n
t
расчет осуществлялся в че-
тыре этапа: 1) выбиралась температура θ
w
(
n
)
поверхности конструкции
на
n
-м шаге, с этой температурой методом установления решались си-
стемы уравнений газодинамики (1), (2) с граничными условиями (5),
(6), а вместо (4) задавались условия
1
( )
0,
;
w n
−
Σ
= θ θ
v
=
(9)
2) в результате вычислялась температура в области
V
1
газа, в том числе
температура θ
e
на внешней условной границе пристеночного вязкого
Рис. 2.
Модель опорной стойки ВЗР ПОС, обтекаемой воздушным потоком,
примененная для решения сопряженной задачи в двумерной постановке


