Ив.И. Захарчук, Ил.И. Захарчук, Ю.Г. Веселов, А.С. Островский
8
Предлагается обобщенная модель клеточного автомата — кортеж
( ), ,
d
R
K G V
= 〈
Φ〉
(2)
где
( )
d
R
G V
— топологическая структура КЛА — бесконечный граф с
множеством вершин
V
группы движений фундаментальной области
R
в пространстве размерности
d
(регулярный граф);
{
}
1 2
, ,...,
r
Φ = ϕ ϕ ϕ
—
локальный оператор переходов ( :
m
i
Q Q
ϕ →
— локальная функция
переходов
i
-й вершины фундаментальной области;
Q
— множество
состояний каждой клетки,
,
,
Q k
Q
= ∅∈
0 1
1
( , ,...,
)
;
m
−
ϕ ∅ ∅ ∅ = ∅
deg ( ) 1,
,
i
i
m v
v V
−
=
+ ∈
— полустепень захода
i
-й вершины фунда-
ментальной области).
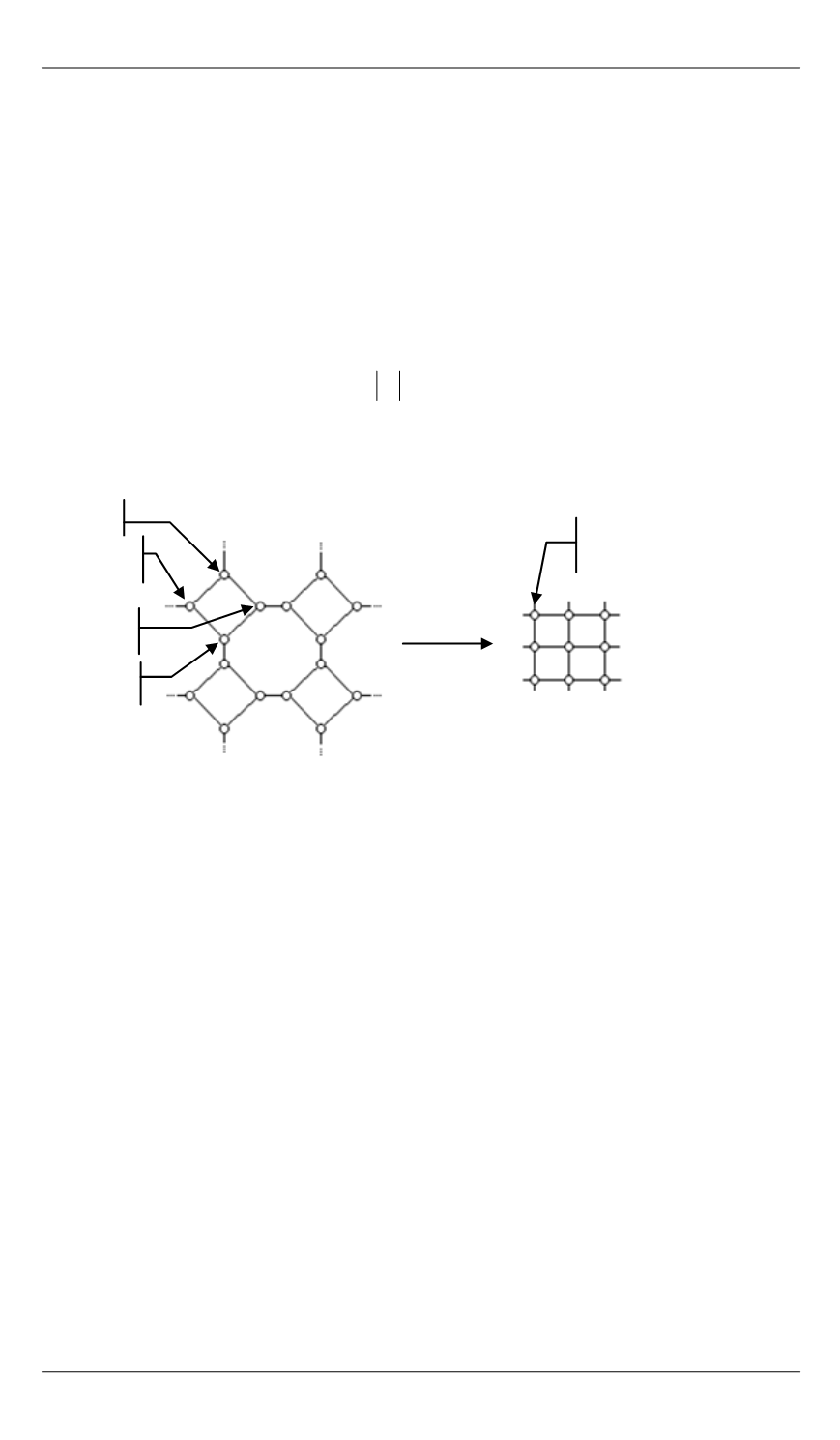
K
1
m
= 3
m
= 4
K
2
K
4
K
3
K
≡
K
1
· K
2
· K
3
· K
4
Рис. 4.
Неоднородные автоматные сети, преобразуемые к классическим КЛА
Обобщенная модель (2) расширяет как множество возможных
топологических структур, так и множество локальных функций пере-
ходов. Она позволяет использовать регулярные графы, сводящиеся к
однородным, и композицию локальных функций.
3.
Алгебра клеточных автоматов
.
Для объединения «элемен-
тарных» клеточных автоматов в функционально более сложные вво-
дятся операции над КЛА:
n
-арные операции параллельного и после-
довательного соединения КЛА, склейки и расслоения КЛА, унарная
операция взятия проекции. Данный «инструментарий» позволяет вы-
делить три подхода к обеспечению функционирования в условиях
сбоев элементов. Первый связан с увеличением числа соседних эле-
ментов. В основе второго лежат идеи корректирующего кодирования
состояний элементов-клеток. Третий метод является комбинирован-
ным и связан с использованием инвариантов при взаимном модели-
ровании клеточных автоматов. Таким образом, возможны следующие
операции над КЛА:


