Ив.И. Захарчук, Ил.И. Захарчук, Ю.Г. Веселов, А.С. Островский
6
ратимости для КЛА размерности 2 и более
( 2)
d
≥
является алгорит-
мически неразрешимой.
Следующий вопрос, связанный с обратимыми КЛА, — это во-
прос о доле их в множестве всех клеточных автоматов. С помощью
усиления теоремы Мура – Майхилла можно показать, что почти все
клеточные автоматы являются необратимыми. В настоящее время в
литературе класс обратимых КЛА часто упоминался как класс малой
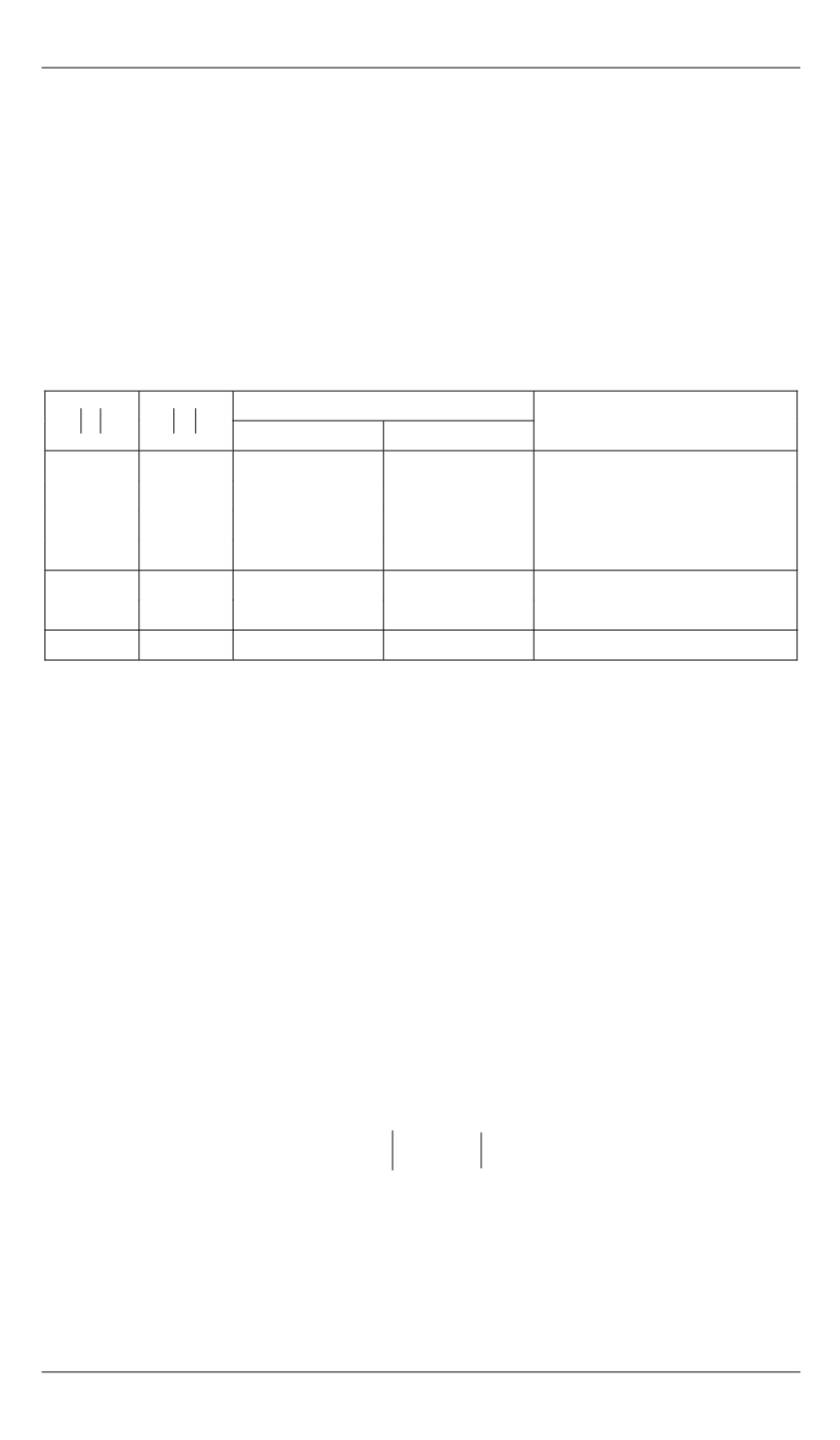
мощности (таблица).
Пример параметров обратимых одномерных КЛА
Q
N
Общее число функций
Число эквивалентных
классов
локальных
обратимых
2
2
16
4
1
3
256
6
1
4
65 536
16
2
5
4,3·10
9
62
7
3
2
19 638
48
3
3
7,6·10
12
1776
101
4
2
4,3·10
9
5184
≈ 60
В [5] было установлено, что асимптотика логарифма числа обра-
тимых клеточных автоматов в любом классе КЛА с фиксированным
шаблоном соседства совпадает с асимптотикой числа всех клеточных
автоматов.
Важным вопросом в исследовании свойства обратимости являет-
ся поиск топологических параметров универсальных КЛА, позволя-
ющих моделировать произвольные клеточные автоматы. При этом в
[6] были сформулированы и доказаны следующие
теоремы
:
1. Любой одномерный КЛА
K
с шаблоном соседства
m
модели-
руется с замедлением, равным
1
m
−
, ординарным КЛА
o
K
с числом
состояний
о
1
.
m
i
i
k
k
=
≤
∑
2. Любой одномерный КЛА
K
моделируется в реальном масшта-
бе времени ординарным КЛА
o
K
с шаблоном соседства
(
)
2
o
2
log 2 2
m m k
≤
−
.
3. Существует универсальный ординарный КЛА
o
u
K
со сложно-
стью
1 16 2.
s
C
= × ×
4. Клеточный автомат с
Z
-шаблоном
Z
K
моделирует поведение
любых двумерных клеточных автоматов с шаблоном Неймана
N
K
с


