Ив.И. Захарчук, Ил.И. Захарчук, Ю.Г. Веселов, А.С. Островский
4
тить, что в общем виде проблема распознавания представимости
КЛА также относится к числу алгоритмически неразрешимых.
Модель.
Формализуем задачу в терминах теории клеточных ав-
томатов.
Клеточный автомат
K
есть упорядоченное множество из четырех
компонент
, , , ,
d
K Z N Q
=
ϕ
(1)
где
d
Z
— множество
d
-мерных векторов с целочисленными коорди-
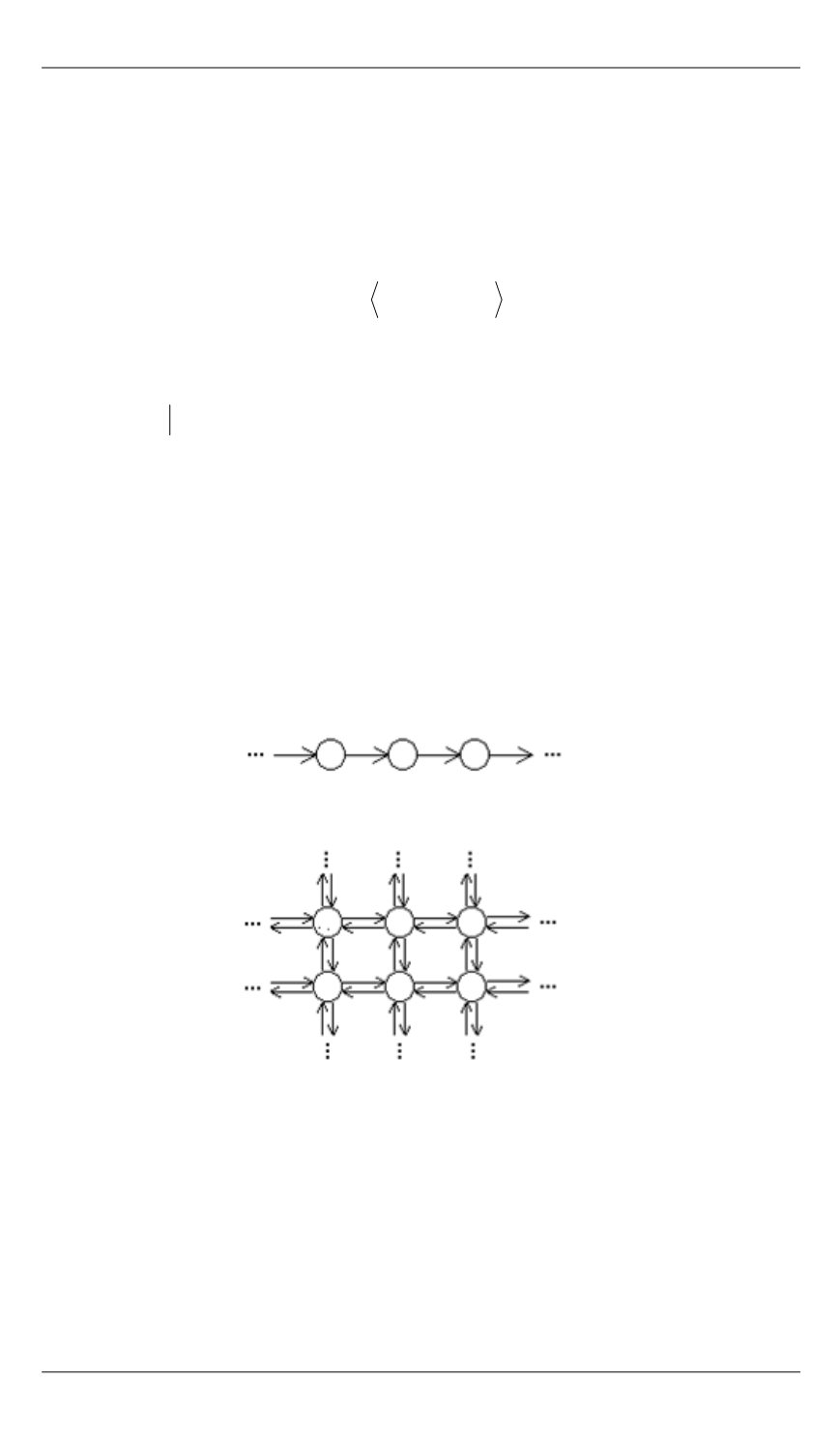
натами — клеточное пространство (рис. 1);
(
)
{
}
1
,...,
,
0 ,
i
i
i
di
i
N n n x x n
= =
∃ =
1,..., ,
i
m
=
— конечное множе-
ство мощности
m
векторов из
d
Z
с нулевым вектором — шаблон
соседства КЛА;
Q
— конечное множество мощности
k
состояний клетки c вы-
деленным состоянием покоя
∅
— алфавит клеточного автомата;
:
m
Q Q
ϕ →
— локальная функция переходов, определенная на
множестве элементов окрестности в дискретные моменты времени
(
)
0 1
1
, ,...,
m
−
ϕ ∅ ∅ ∅ = ∅
.
Рис. 1.
Варианты клеточного пространства
Состояние всех клеток на момент времени
t
образует текущую
конфигурацию
:
.
d
t
c Z Q
→
Применение локальной функции перехо-
дов к текущей конфигурации задает глобальную функцию переходов
( )
1
.
j
j
c
f c
+
=
d
= 1
d
= 2


