Обеспечение информационной защиты беспроводных сенсорных сетей…
5
Упорядоченная совокупность конфигураций, получаемая из
начальной последовательным применением глобальной функции пе-
реходов,
образует
эволюцию
e
клеточного
автомата
0 1
, ,...,
e c c c
τ
= <
>
. В общем случае
0
card
e
=ℵ
.
Одномерные клеточные автоматы, у которых
2
m
=
или
2
k
=
,
будем называть
ординарными
. Шаблон, у которого по каждой коор-
динате имеется единственный сосед, находящийся на единичном рас-
стоянии от центрального, будем называть
Z-шаблоном
, а шаблон, об-
разующий
d
-мерный единичный куб, —
S-шаблоном
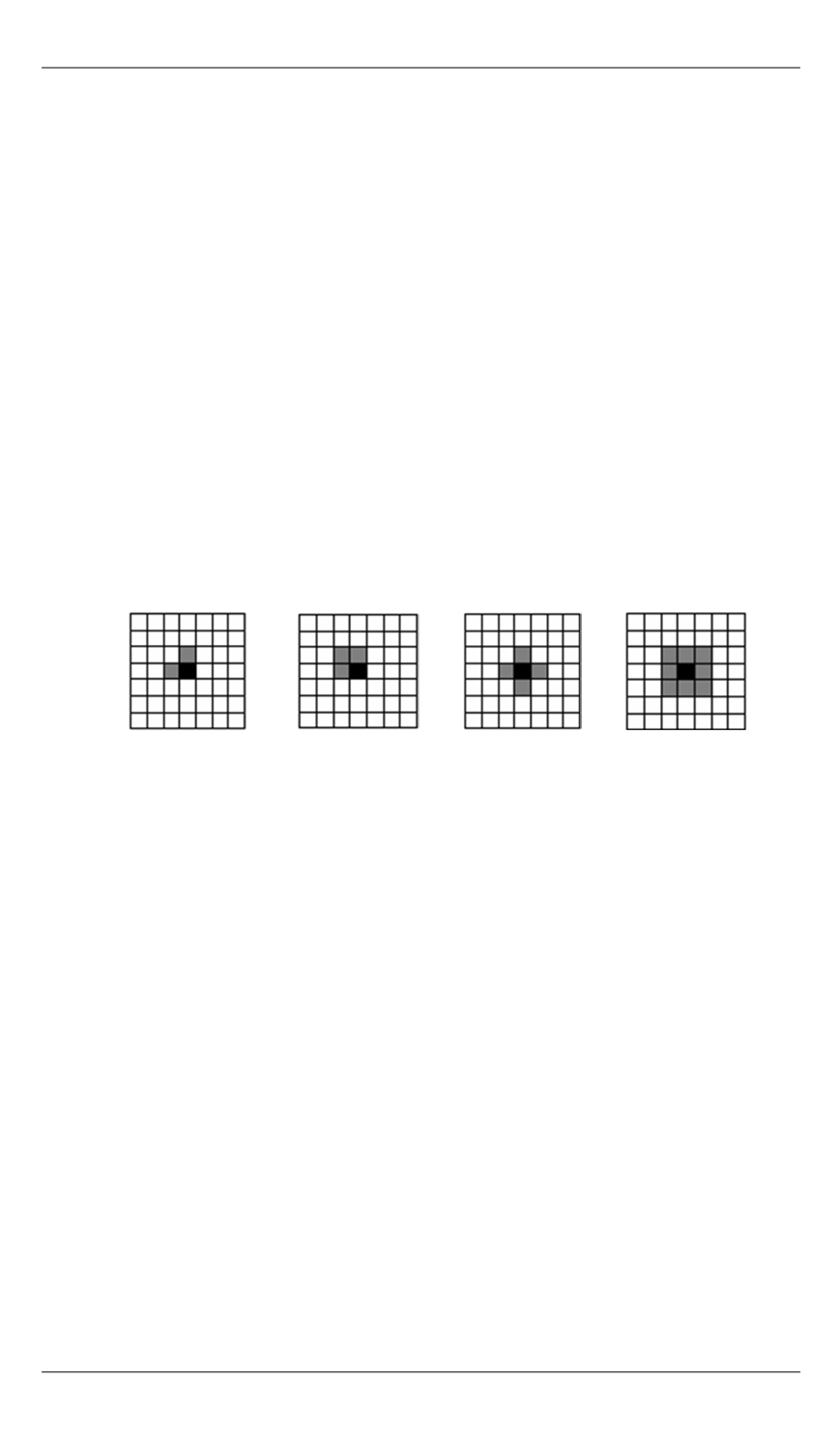
. Для двумерного
КЛА (рис. 2)
Z
-шаблон — ( 2,
3)
d m
= =
,
S
-шаблон — ( 2,
4)
d m
= =
,
N
-шаблон Неймана — ( 2,
5)
d m
= =
,
М
-шаблон Мура — ( 2,
d
=
9)
m
=
. Кроме числа элементов
m
шаблоны двумерных КЛА будем
характеризовать сторонами прямоугольника, описывающего данный
шаблон, —
x
и
.
y
Рис. 2.
Варианты шаблонов для двумерного КЛА
По аналогии с введенной Шенноном сложностью универсальных
машин Тьюринга произведение
s
C d m k
= × ×
задает сложность уни-
версальных КЛА.
Клеточный автомат
*
K
моделирует поведение клеточного автома-
та
K
с замедлением
n
, если для любой эволюции
,
e E
∈
допускаемой
клеточным автоматом
K
, существует гомоморфизм
*
:
,
h E E
→
причем
( )
*
.
j
nj
c h c
=
При
1
n
=
будем говорить, что моделирование осуществ-
ляется в реальном времени.
Решения.
1.
Инварианты
.
Первым значимым классом, для кото-
рого были получены продвижения в задаче распознавания свойства
обратимости, стал класс одномерных КЛА. В [3] было установлено,
что в этом классе существует алгоритм для распознавания обратимо-
сти. В той же работе высказана гипотеза, что для многомерных КЛА
свойство обратимости также разрешимо, и даже было предложено
попытаться обобщить на них технику одномерного случая. Однако в
работе [4] было установлено, что задача распознавания свойства об-
Z
S
N
M


