Разработка математической модели высокомоментного синхронного двигателя при проектировании прецизионных приводов - page 5

5
Разработка математической модели высокомоментного синхронного двигателя...
поля). В модели для описания функции Hм(B) используется кусочно-
параболическая аппроксимация табличных значений.
Магнитодвижущая сила  
E Iw
МД МД , создаваемая постоянным маг-
нитом с индукцией B r, находится как
 
0
r B l
Iw 

МД ,
где l – длина магнита по направлению намагниченности.
Сумма всех магнитных напряжений и магнитодвижущих сил по
замкнутому контуру эквивалентной электрической схемы замещения
равна нулю. Для решения нелинейного уравнения может быть исполь-
зован итерационный алгоритм поиска. Еще один простой способ опре-
деления магнитного потока заключается во введении в контур эквива-
лентной электрической схемы замещения фиктивной индуктивности L.
В этом случае переменной Фм присваивается начальное значение как
переменной состояния. По заданному значению Фм вычисляется сумма
всех магнитных напряжений на воздушных участках цепи Uв и напря-
жений на участках магнитопровода Uм. Производная Фм составляет
2
М М В В Ф d E U U
dt L
 
 .
В результате численного интегрирования рассчитывается установив-
шееся значение переменной Ф м.
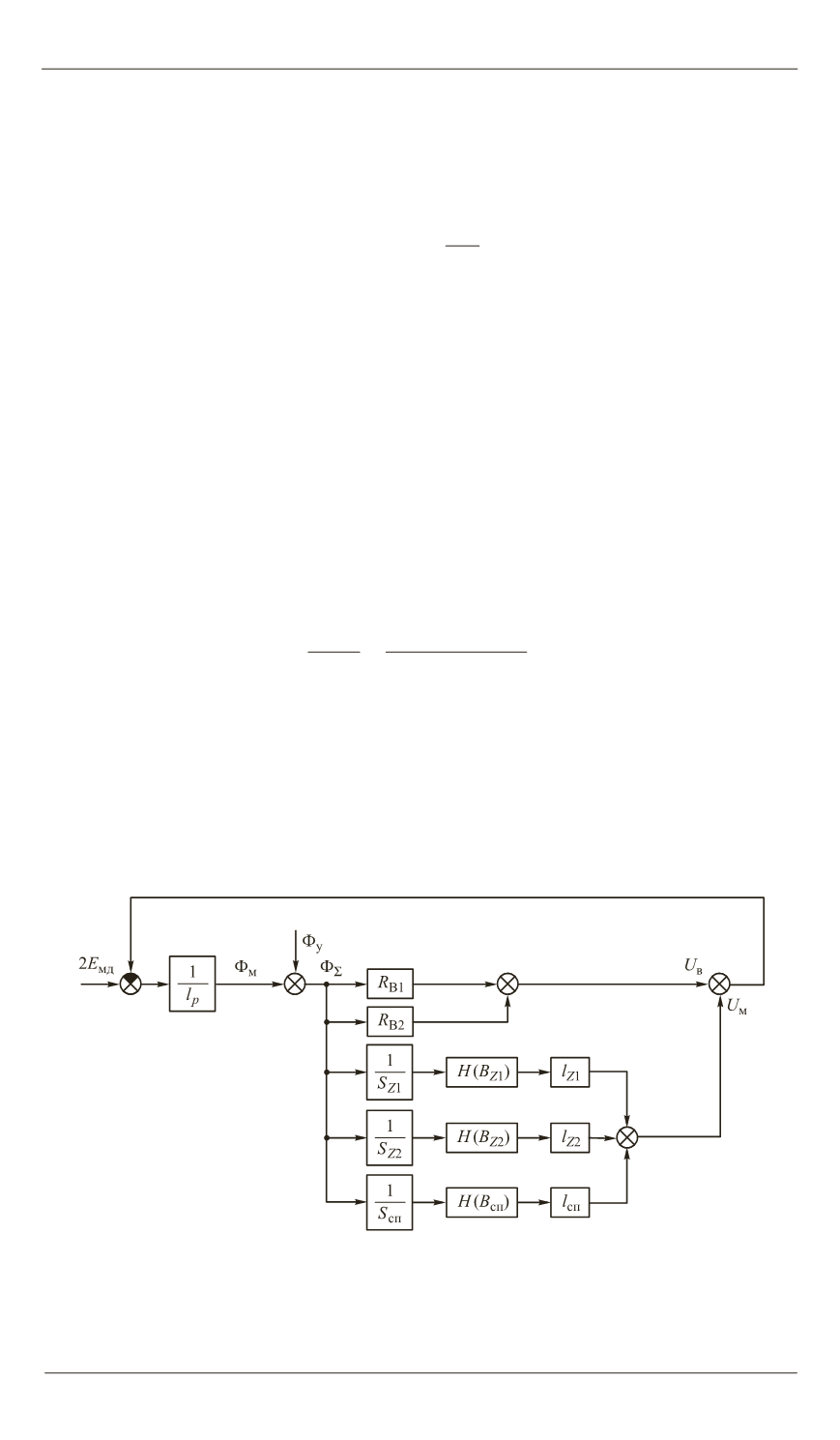
Математическая модель для определения магнитного потока в зуб-
це приведена на рис. 3. Падением магнитного напряжения на роторе
в этой схеме пренебрегаем в силу достаточно большой площади сечения
участка магнитопровода и его малой длины.
Рис. 3. Математическая модель для определения магнитного потока в зубце:
BZ1, BZ2, Bсп – индукция в зубцах фаз В и А, в спинке статора; SZ1, SZ2, Sсп и lZ1,
lZ2, lсп – эффективные площади магнитопровода указанных зубцов, спинки
статора и длины соответствующих участков магнитопровода