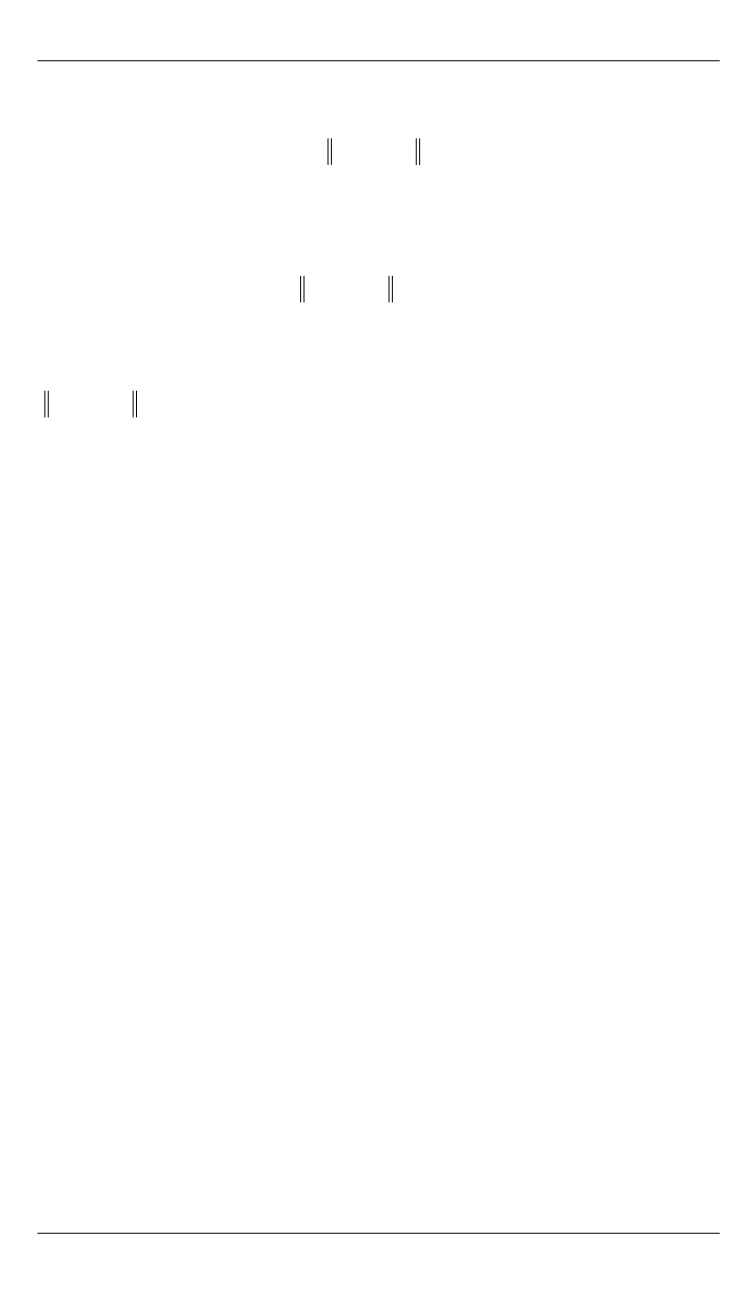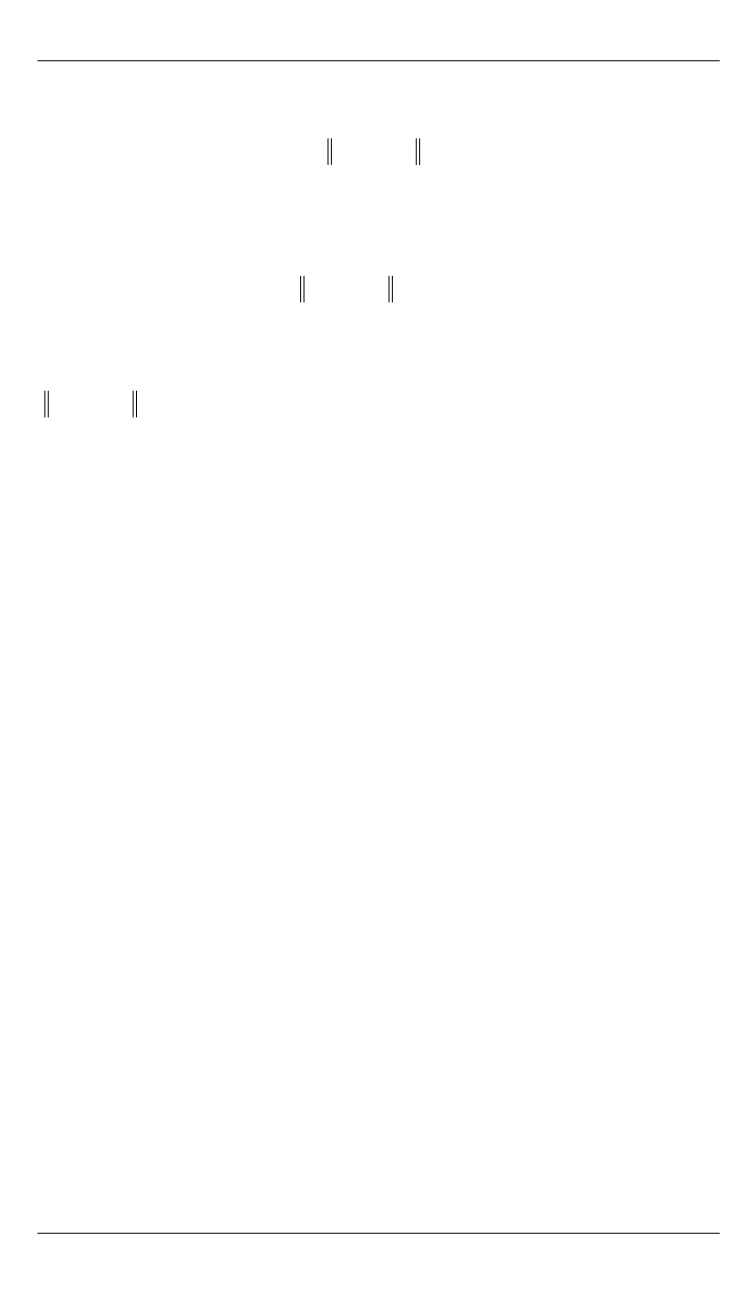
Современные методы расчета вариообъективов
5
В работе [22] для решения данной проблемы предлагается выби-
рать вектор изменения параксиальных величин для двух соседних
позиций бесконечно малым:
1
0
k
k
+
− →
P P
и затем для определения
d
минимизировать функцию:
[
] [
]
т
( )
( )
( )
.
k
k
d
= −
−
Φ d P d P P P
(3)
На практике же величина
1
k
k
+
−
P P
имеет конечное значение, и при
неправильном ее выборе возможна ситуация, когда решения будут
лежать на разных кривых. Такой подход приводит к большим вычис-
лительным затратам, поскольку число позиций
K
→ ∞
при
1
0.
k
k
+
− →
P P
Существенным недостатком метода является то, что
он не позволяет проводить оптимизацию по
,
φ
так как каждое реше-
ние
d
, найденное с помощью минимизации (3), зависит от предыду-
щего. Кроме того, увеличение числа позиций
K
приводит к увеличе-
нию числа неизвестных
d
, поскольку
d
зависит от номера
k
позиции.
Предложенный в работах [19–21] метод свободен от указанных недо-
статков. Рассмотрим этот метод.
Каждое расстояние
d
вектора
d
есть функция от фокусного рас-
стояния системы:
( ),
d d f
= ′
либо в параметрическом виде
( ),
d d m
=
( ),
f
f m
=′
′
где
m
— параметр, определяющий положение компонен-
тов. Представим данные функции в виде разложения по базисным
функциям
0
( )
( ),
N
i i
i
d x
a F x
=
=
∑
(4)
где
i
a
— коэффициенты разложения;
N
— число членов разложения;
( )
i
F x
— базисная функция
i
-го порядка;
x
— аргумент базисной
функции, может быть равен
m
или
f
′
в зависимости от того, что
более удобно для каждой конкретной задачи.
Подставив разложение (4) в систему (1), получим
( , ) ( ).
=
P a φ P x
(5)
В результате вместо вектора расстояний
d
необходимо определить
коэффициенты
a
разложения по базисным функциям. При решении
системы (5) численными методами не возникает проблемы согласо-
вания корней, так как они заведомо принадлежат одной кривой, уве-
личение числа
K
позиций не приводит к увеличению числа неизвест-
ных, кроме того, появляется возможность минимизировать оптиче-
ские силы
.
φ