Метод компьютерного синтеза микроголограмм Фурье и оптическая система записи…
3
ницей входных данных τ(
x
,
y
)
задается дискретно в виде матрицы τ(
k
,
l
) отсчетов
с шагом дискретизации ∆
x
, ∆
y
[4], то
(
)
( ) (
)
0 0
,
,
,
,
y x
NN
k l
x y
k l
x x y y
= =
τ
= τ δ −Δ −Δ
∑ ∑
(4)
где
N
x
,
N
y
— числа отсчетов, определяемые размерами исходных объ-
ектов
A
и
B
:
,
x
A N
x
=
Δ
.
y
B N
y
=
Δ
(5)
Если шаг дискретизации ∆
x
, ∆
y
удовлетворяет условию
max
max
1
1
;
,
2
2
x
y
x
y
Δ =
Δ =
ν
ν
(6)
где 2
ν
x
max
, 2
ν
y
max
— размеры ПЧС страницы входных данных,
то
матрица отсчетов τ(
k
,
l
)
полностью определяет исходную непрерыв-
ную функцию τ(
x
,
y
). Тогда для дискретного объекта (4) распределе-
ние комплексных амплитуд в плоскости МГФ (в плоскости фурье-
спектра) имеет следующий вид:
(
)
( )
1 1
сп
max
max
0 0
,
, exp 2
.
2
2
y x
N N
y
x
x y
x
y
k l
T
k l
i
k
l
− −
= =
⎡
⎤
ν
ν
⎛
⎞
ν ν =
τ
⋅ π
+
⎢
⎥
⎜
⎟
ν
ν
⎢
⎥
⎝
⎠
⎣
⎦
∑ ∑
(7)
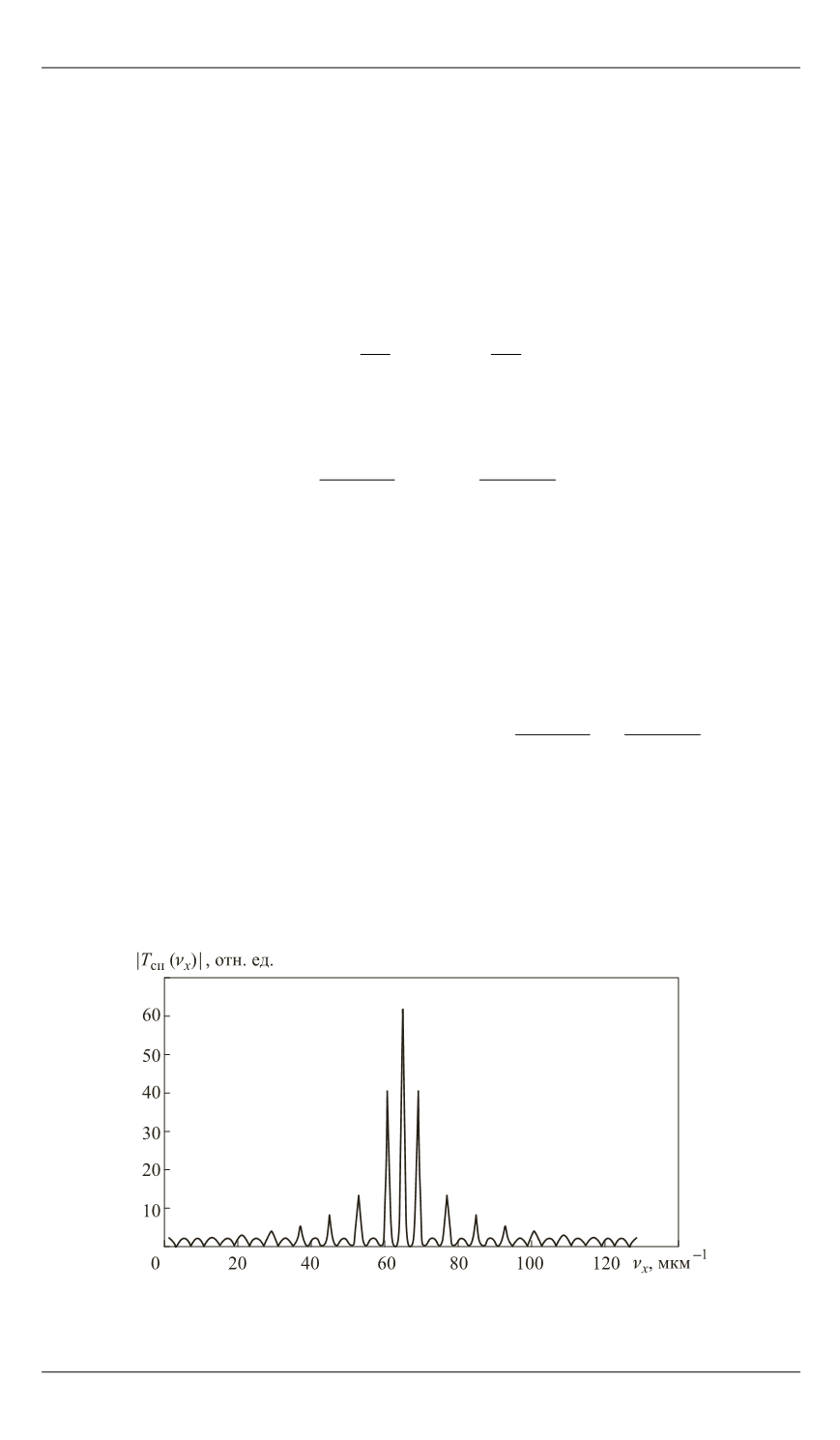
На рис. 1 приведена зависимость модуля комплексной амплитуды
МГФ (7) от пространственной частоты
ν
x
. Видно, что распределение
модуля комплексной амплитуды имеет большой динамический диа-
пазон, для «сглаживания» которого на страницу входных данных
накладывают кодирующую фазовую маску (КФМ) (рис. 2).
Рис. 1.
Зависимость модуля комплексной амплитуды МГФ от простран-
ственной частоты


