Моделирование спекания с помощью теории пластичности
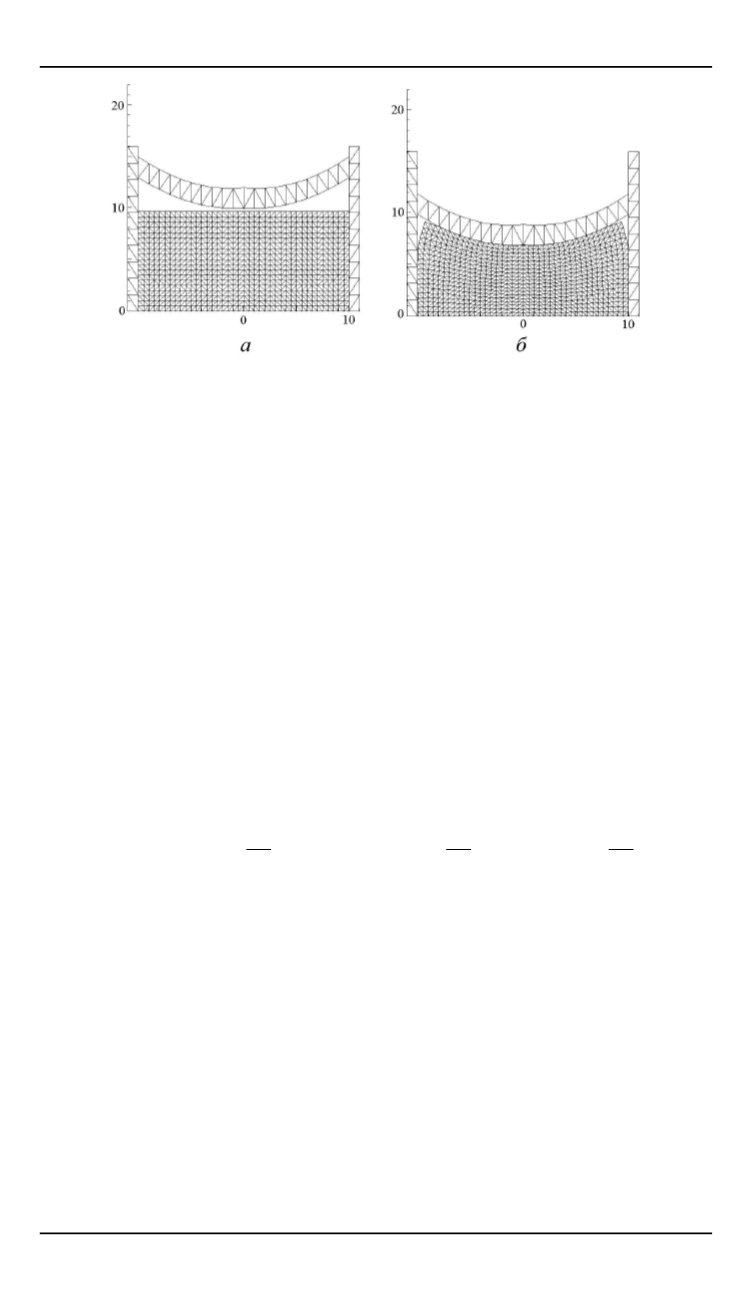
Рис. 6.
Стадия холодного прессования порошка в цилиндрической пресс-форме
подвижным сферическим штампом при
= 0
(
а
) и
= 38
(
б
)
Пусть в начальный момент времени
= 0
в печь цилиндриче-
ской формы насыпают композитный порошок, пористость которого
плоским штампом доведена до значения
w
0
= 0
,
5
. Это значение со-
ответствует начальному состоянию. Далее рассчитывают параметры
процесса холодного прессования с помощью сферического штампа-
крышки, движущегося вниз и деформирующего прессовку до неод-
нородного состояния (см. рис. 6) для момента времени
= 30
. За-
тем штамп убирают вверх, а прессовку (green body) выдерживают до
= 40
. Далее печь нагревают до температуры
0
, которая сохраняется
постоянной до момента времени
= 140
и поддерживают напряжение
спекания, зависимость которого от пористости принимали в виде
s
w
=
*
( )
w
= (
−
2
) (
3
−
)
w
.
Вначале прессовка не сопротивляется деформации, модули упру-
гости и предел текучести ее материала зависят от пористости как
= 975
(︁
1
−
w
w
0
)︁
,
m
= 369
(︁
1
−
w
w
0
)︁
,
= 1
−
w
w
0
,
где
w
0
= 0
,
5
— начальная пористость. По мере уменьшения пористо-
сти свойства упругости нарастают.
Распределение пористости и пластической работы после стадии
холодного прессования показано на рис. 7. В процессе холодного
прессования благодаря пластическому течению прессовка нагревается
за счет работы пластической деформации. Полученное в предположе-
нии, что работа деформации перешла в теплоту и диффузия теплоты
отсутствует (
= 0
), распределение тепловой внутренней энергии
(
) после прессования показано на рис. 8,
а
. Полагаем, то этой
теплоты недостаточно для расплавления легкоплавкой компоненты.
Достигнув предельного положения, сферический штамп начинает
обратное движение и до момента времени
= 50
напряжения и ма-
лые упругие деформации в композите немного уменьшаются, но не
9


