В.И. Вишняков, Л.Д. Покровский
4
решение которого, удовлетворяющее начальному условию
0 0,
y
имеет вид
2
ln
.
s
s
s s
s
y y
t
y d y d y y y d
d y
(6)
Отметим, что
s
y t
y
при
t
, т. е. переход из одного стаци-
онарного состояния в другое происходит за бесконечное время. Реше-
ние поставленной задачи определяется выражениями (5) и (6). Отме-
тим также, что оно единственное вследствие теоремы существования и
единственного решения задачи Коши.
Для числовой оценки решения уравнение (6) удобно записать в
безразмерном виде, вводя такие же, как в работе [5], переменные:
,
y Y
d
0
,
p
p
*
,
t
t
t
2
*
2
d t
,
0
1,
s
s
p
p
1 1.
s
s
Y
Уравне-
ние (6) в безразмерном виде:
1 1 2
1 ln
.
1
s
s
s s
s
Y Y
t
Y Y Y Y Y
Y
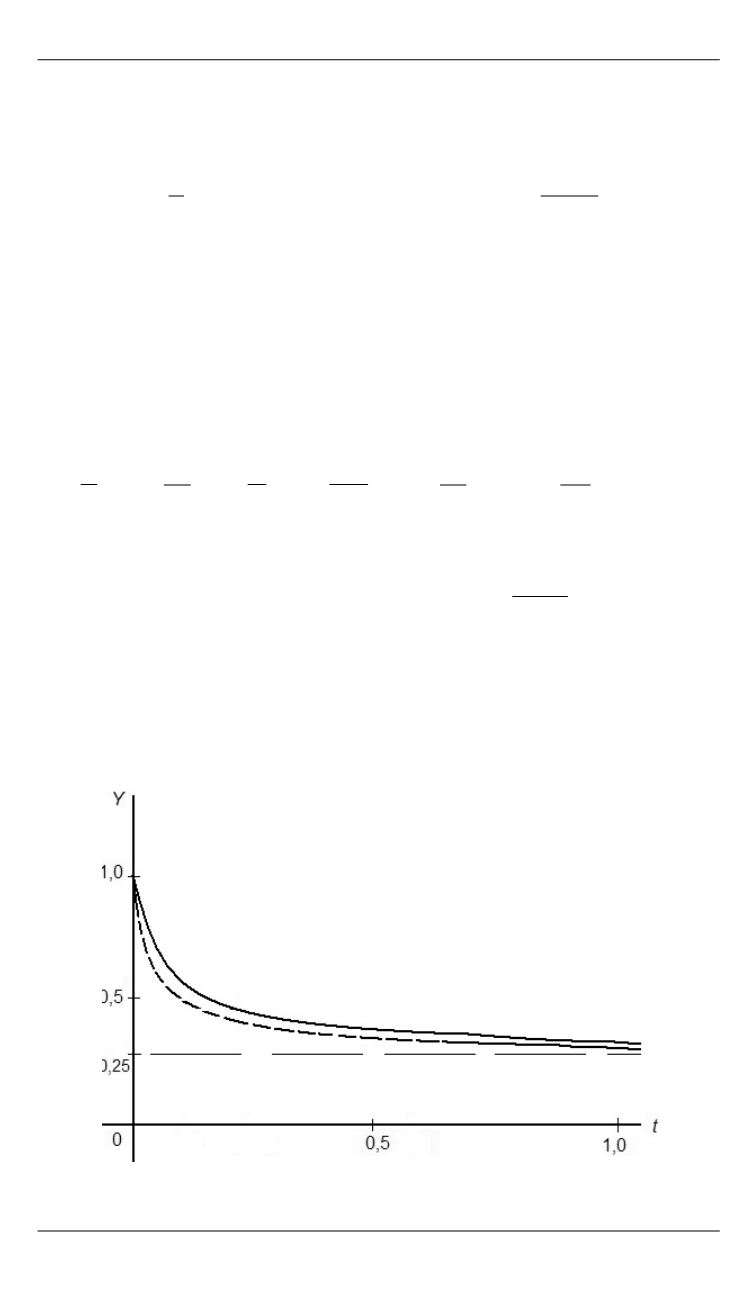
На рис. 2 приведена зависимость
y t
при значениях
1/ 4,
s
Y
0 1.
Y
Она незначительно отличается от аналогичной кривой из
работы [5], отмеченной на рис. 2 пунктирной линией.
Рис. 2.
Зависимость
y t


