В.И. Вишняков, Л.Д. Покровский
2
разработаны приближенные и численные методы, в том числе осно-
ванные на модификации уравнения Шведова – Бингама (см., напри-
мер, работу [5]). Причем уравнения, описывающие движения среды в
вязких и квазитвердых зонах, оказываются частично расщепленными.
Это позволяет, оставаясь в рамках классической бингамовской реоло-
гической модели, при некоторых естественных дополнительных усло-
виях рассмотреть отдельно движение квазитвердой зоны, найти точное
решение задачи и установить его единственность. Такие решения
представляют определенный интерес, например, в случае, если ква-
зитвердая зона занимает (по ширине) большую часть канала.
Цель данной работы – получить решение задачи об одномерном
течении бингамовской среды с реологическим законом (1) в беско-
нечном плоском канале под действием скачкообразно изменяющего-
ся градиента давления.
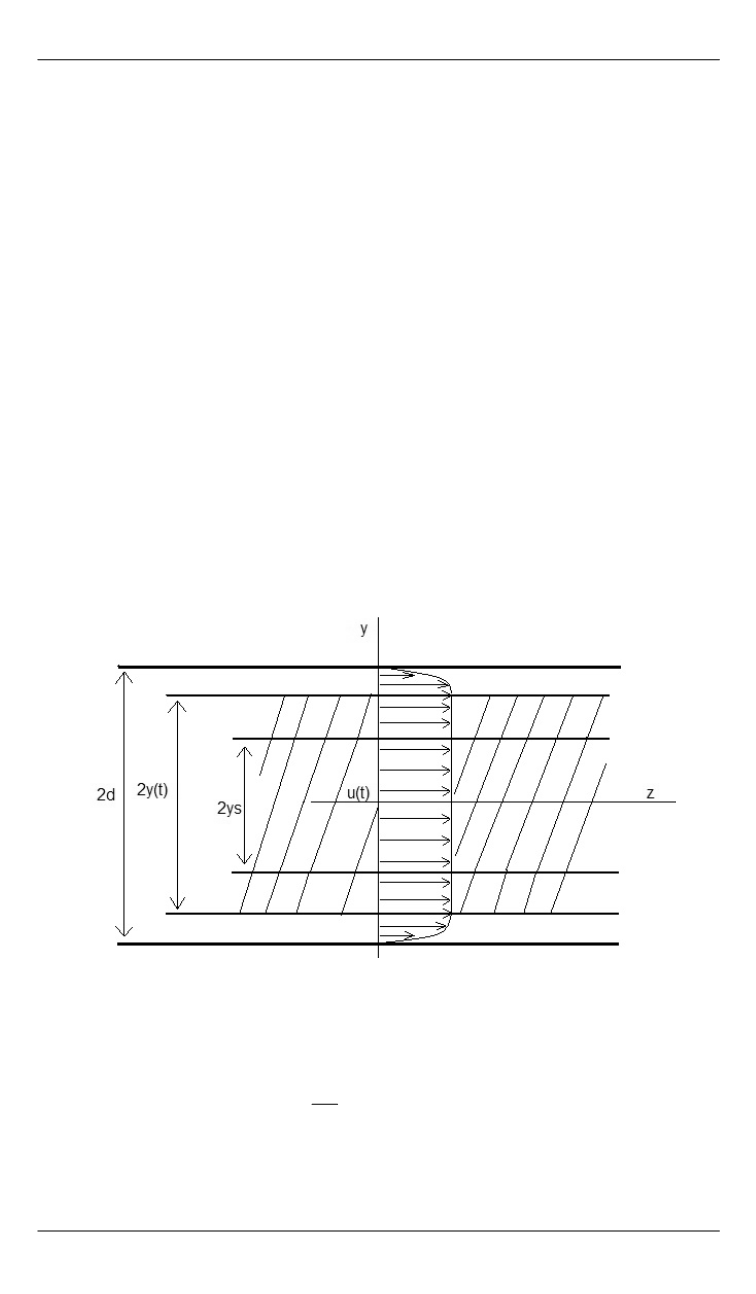
Решение задачи.
Схема течения приведена на рис. 1, где направле-
ние течения совпадает с осью
,
z
координата
y
отсчитывается от сере-
дины канала,
y t
определяет положение границы квазитвердой зо-
ны,
d
– полуширина канала (вследствие симметрии рассматривается
только верхняя половина канала).
Рис. 1.
Схема течения
Уравнение движения, записанное для элемента квазитвердого яд-
ра длиной
Δ
z
, имеет вид
0
Δ
Δ ,
du m t
py t
z
dt
где
Δ ,
m t
y t z
плотность среды;
u t
cкорость движе-
ния квазитвердого ядра в момент времени
t
.


