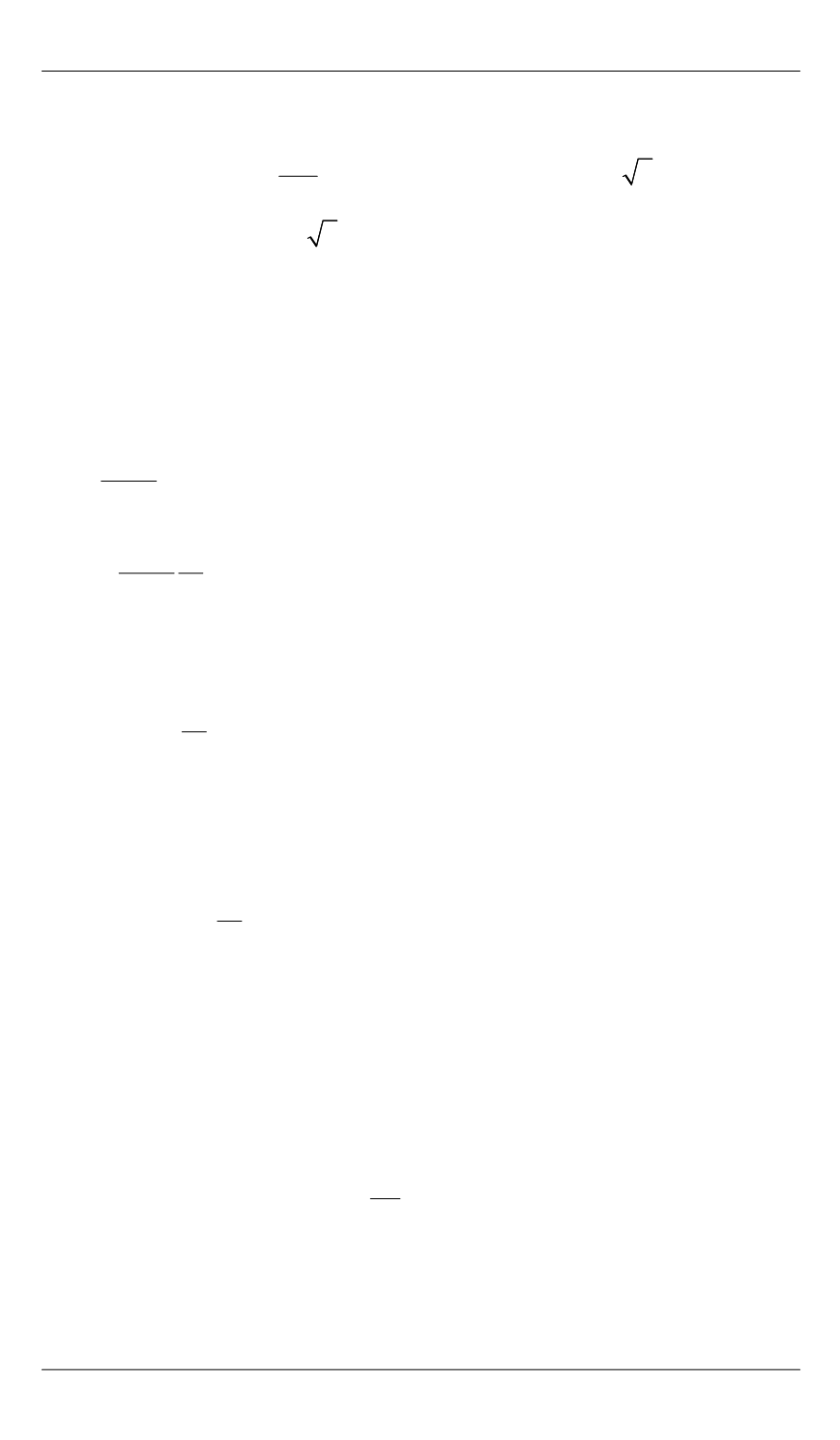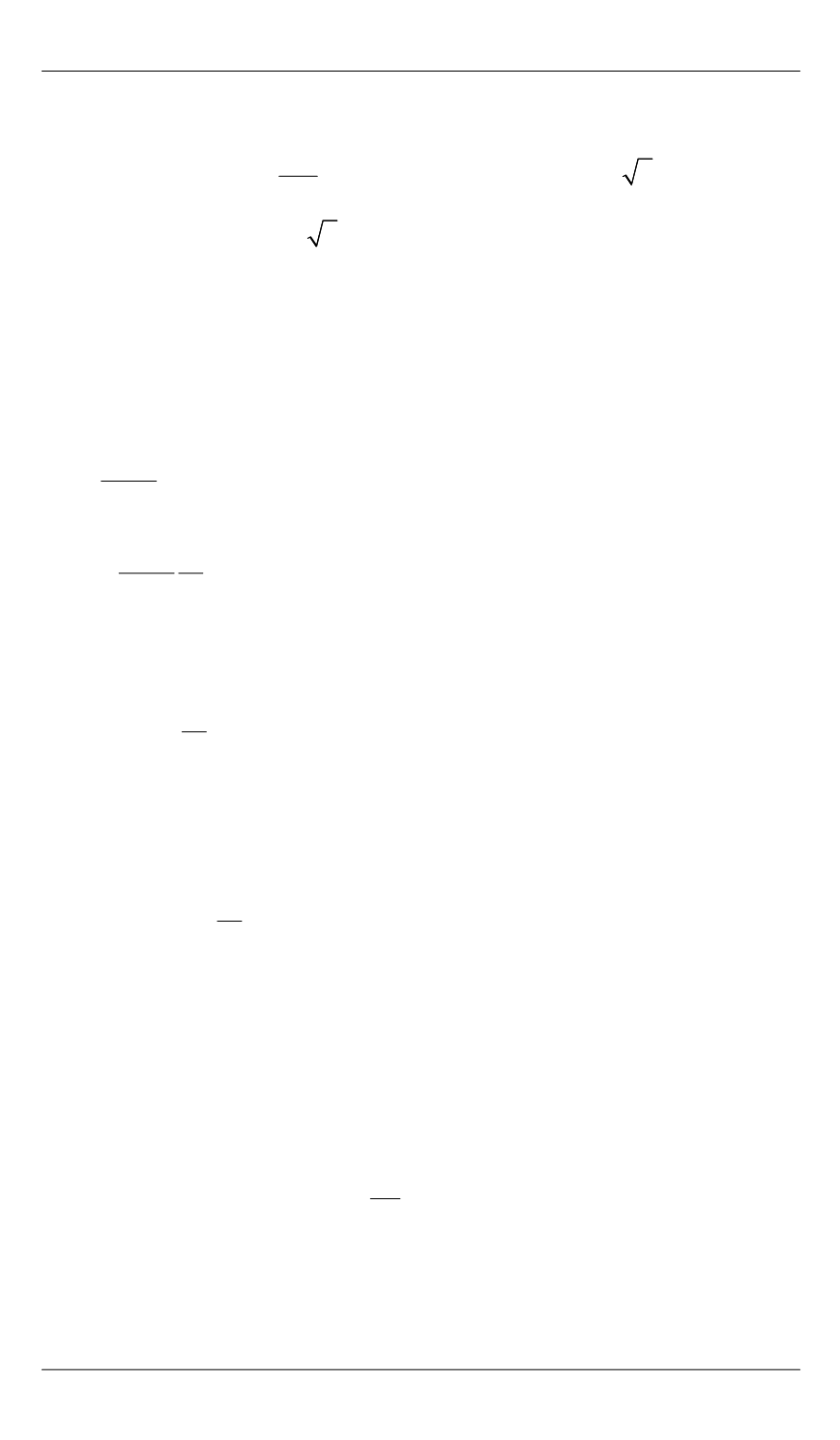
Описание свойств электронного газа вблизи поверхности металла
5
допускает аналитическое представление
1
2
( )
cos cos 2cos 2 exp 2
3
4cos 2 2 sin ( ) .
V r
A
kx ky
kz
k z
k
kz
kz
z
(6)
Ограничиваясь в выражении (4) первым порядком градиентного
разложения (2) для пространственной плотности кинетической энер-
гии
t
[
n
2
](
r
1
,
r
2
), можно перейти к алгебраическому уравнению отно-
сительно
(0)
2 1 2
( , ):
n r r
1 1 1 2
1/3
2/3
4/3
4
(0)
(1)
(1)
2 1 2
2 1 2
2
1 ( )
( )
1
1 4 18
( )
( , )
( , )
,
115
d
V r V r
N
C p
n r r
n r r
N
допускающему аналитическое решение относительно
(1)
2 1 2
( , )
n r r
:
1/3
2/3
4/3
(1)
4
(0)
(1)
2 1 2
2 1 2
2
1 1 1 2
15
( , )
18
( )
( , )
( ) ( ) .
4
d
n r r
C p
n r r
V r V r
Условие постоянства нормировки
n
2
(
r
1
,
r
2
) приводит к тому, что
поправка
(1)
2
оказывается равной нулю, и окончательно получаем
1/3
2/3
4/3
(1)
4
(0)
2 1 2
2 1 2
1 1 1 2
15
( , )
18
( )
( , )
( )
( )
4
d
n r r
C p
n r r
V r V r
,
где потенциал
V
1
(
r
) определен выражением (6), а для
(0)
2 1 2
( , )
n r r
мож-
но применить результаты работ [2–4]. Амплитуду
А
осцилляций
плотности положительного заряда ионов кристаллической решетки
можно оценить с использованием ее периодических потенциалов и
уравнения Пуассона
V
(
r
) = –4
n
+
(
r
). При таком подходе
1
0
1
( )
( )
( )
4
n r
V r n r
,
где
V
(
r
) – периодический потенциал кристаллической решетки
(потенциал Ашкрофта [5], экранированный кулоновский потенци-
ал и т. д.).