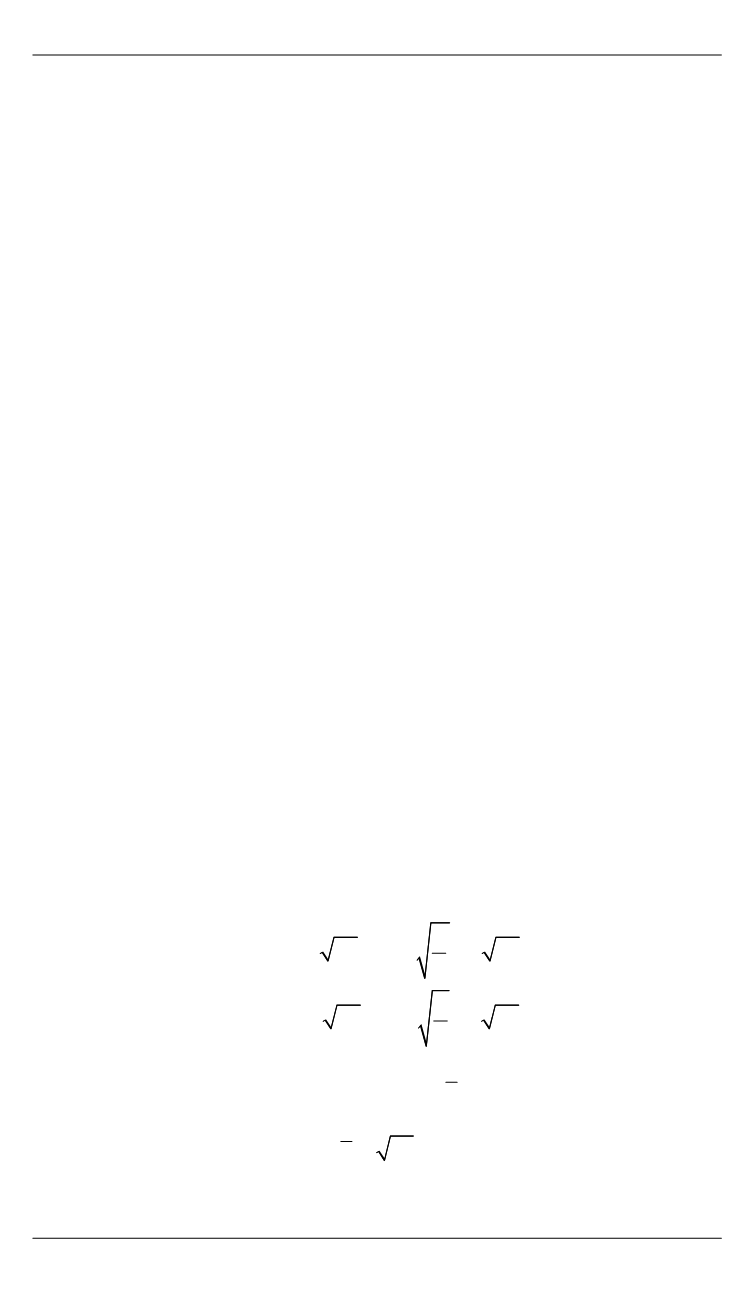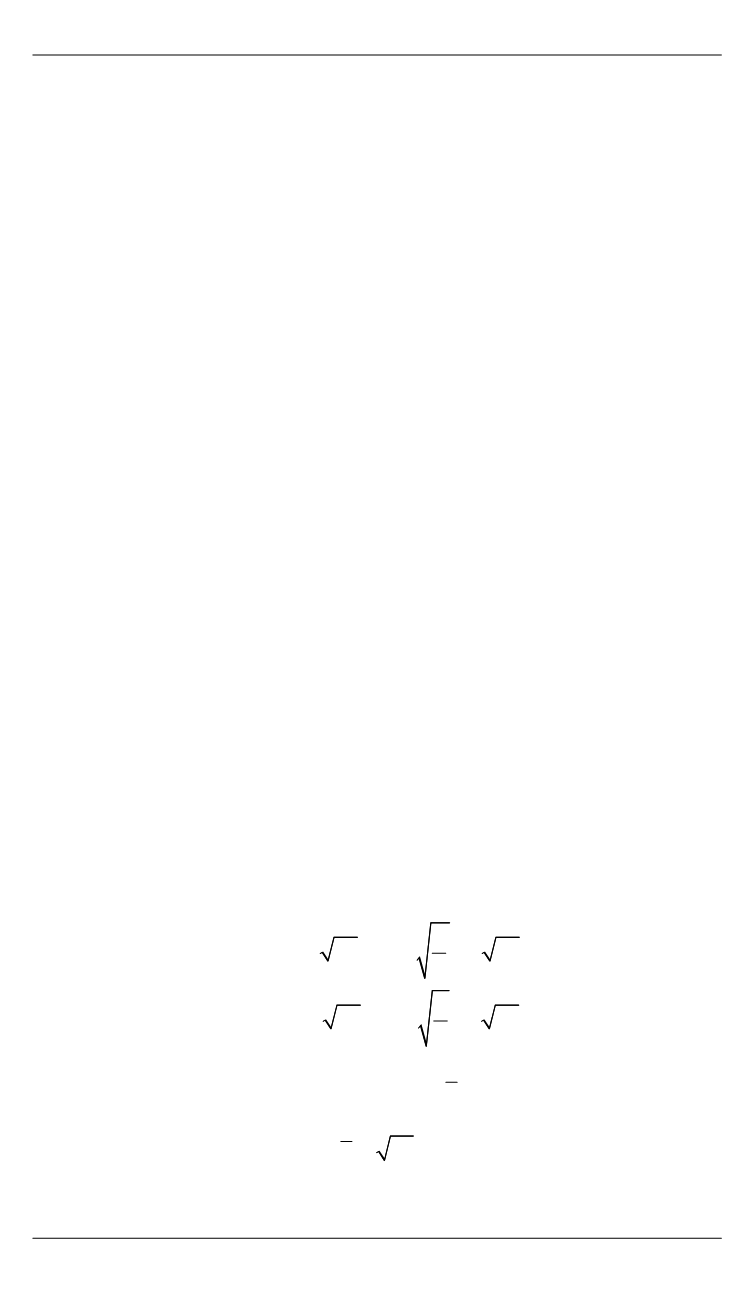
И.В. Дубограй
,
Л.Н. Дьякова
,
В.Ю. Чуев
2
вых единиц) пропорциональна не самому случайному числу сохра-
нившихся боевых единиц, а его среднему значению (математическо-
му ожиданию).
Обозначим через
x
и
y
средние численности боевых единиц,
сохранившиеся к моменту времени
t
, их производные по времени со-
ответственно
x
и
'
y
, вероятности поражения боевой единицы одной
стороны одним выстрелом другой –
x
P
и
y
P
, скорострельности бое-
вых единиц сторон соответственно
x
и
.
y
Произведения
x x
V P
и
y y
U P
назовем эффективными скорострельностями боевых еди-
ниц сторон.
Рассмотрим так называемый высокоорганизованный бой, т. е. стре-
ляющие видят поражена цель или нет, и мгновенно переносят огонь
на непораженную. Тогда процесс боевых действий можно описать
хорошо известной [5–9] системой дифференциальных уравнений:
,
x uy
y vx
(1)
с начальными условиями
0
0
0
0
0
0,
,
.
t
x t
x y t
y
(2)
Если считать эффективные скорострельности боевых единиц сто-
рон в течение боя постоянными, что при исследовании многих бое-
вых ситуаций является вполне приемлемым, т. е.
const,
const,
u
v
то система уравнений с начальными условиями (2) имеет следующее
решение:
0
0
0
0
,
.
u
x x ch uvt
y sh uvt
v
v
y y ch uvt x sh uv t
u
(3)
При введении приведенного времени
,
t
такого что
,
t
uv t
(4)
и параметра соотношения сил