Опыт преподавания дискретной математики: сети Петри
9
Переходы (действия):
1) подать изделие на вход в систему;
2) удалить готовое изделие из системы;
3) автомату
M
1
начать обработку;
4) автомату
M
1
закончить обработку;
5) автомату
M
2
начать обработку;
6) автомату
M
2
закончить обработку.
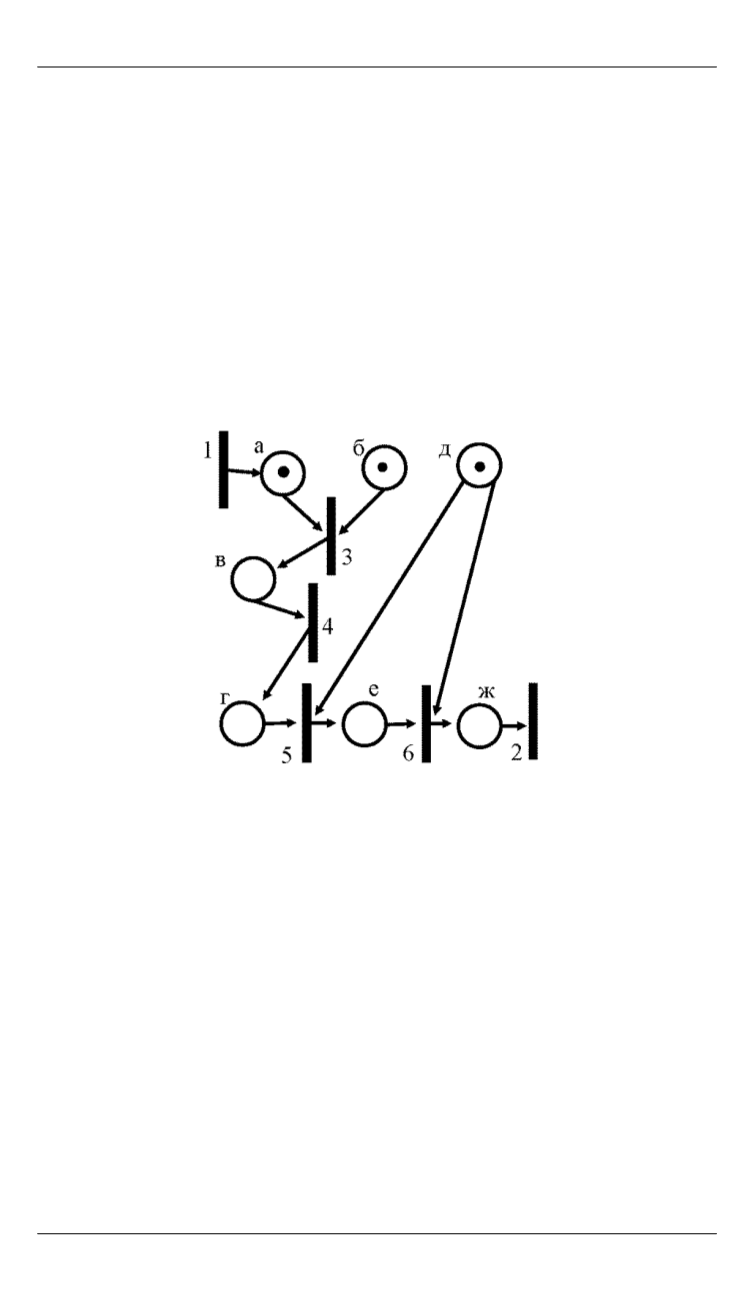
Соответствующая сеть Петри (уже с маркировкой) изображена на
рис. 15 (пусть читатель проверит). Расположив позиции в алфавит-
ном порядке а–ж, получаем, что последовательность маркировок и
переходов имеет вид
(1100100), 3; (0010100), 4; (0101100), 5; (0100010), 6; (0100001).
Рис. 15
Таким образом, рассмотрена работа двух обрабатывающих
устройств. Более сложная (и более реалистическая) ситуация возникает
тогда, когда имеются еще операторы, обслуживающие эти устройства.
Однако операторов можно причислить к «обрабатывающим устрой-
ствам», при этом возникает более сложная система взаимодействия
«обрабатывающих устройств», которая также может быть описана с
помощью сетей Петри. Таким образом, сети Петри предоставляют ши-
рокие возможности «моделировать» сложные системы.
Заключение.
В статье указаны элементы, из которых состоит
сеть Петри, и описана ее работа, а также отмечено важное и интерес-
ное обстоятельство: работа сети Петри может быть описана c помо-
щью линейных операций над векторами, координаты которых —
натуральные числа. Эти простые операции привели к содержатель-
ному анализу, имеющему важные приложения, и наглядному пред-
ставлению сложных систем.


