Опыт преподавания дискретной математики: сети Петри
7
Пример 2.
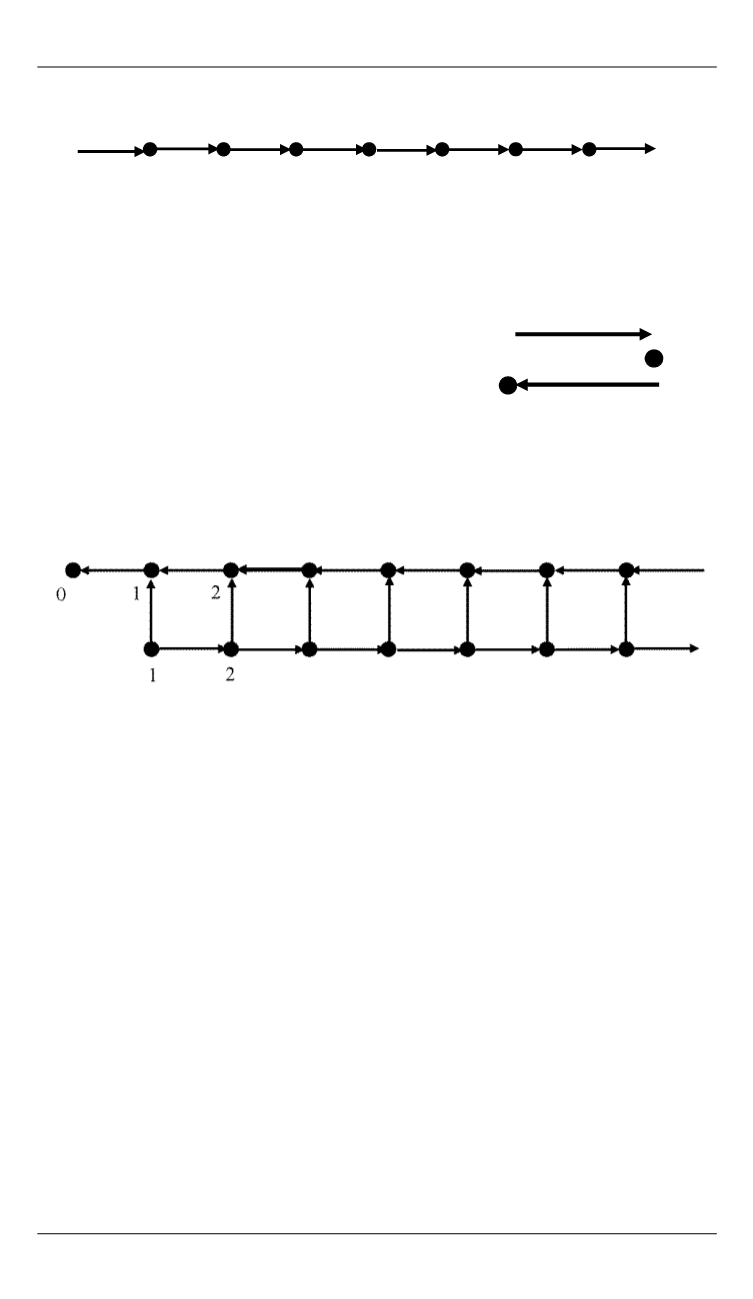
Для сети на рис. 3 с
начальной маркировкой
= (1, 0, 0)
граф
G
(
C
,
) имеет вид, изображенный
на рис. 14. Заинтересованный читатель
может проверить это, а также описать
дерево
T
(
C
,
). Впрочем, целесообразно
приступить к этой работе после разд. 5,
в котором дается удобный вычисли-
тельный способ анализа маркированных
сетей Петри.
Рис. 14
5. Векторный язык для описания маркированной сети Петри.
Пусть
p
1
, …,
p
m
— все позиции сети Петри;
t
1
, …,
t
n
— все переходы.
Для каждого перехода
t
k
введем вектор
vec
a
k
=
(
a
k
(1), …,
a
k
(
m
)), где
a
k
(
r
) — число ребер, идущих от
p
r
к
t
k
. Аналогично возьмем вектор
vec
b
k
= (
b
k
(1), …,
b
k
(
m
)), где
b
k
(
r
) — число ребер, идущих от
t
k
к
p
r
.
(Разумеется,
a
k
(
r
)
= 0, если позиция
p
r
не является входящей в пере-
ход
t
k
; аналогично
b
k
(
r
) = 0, если позиция
p
r
не является выходящей
из
t
k
.) Возьмем некоторую маркировку
и запустим переход
t
k
. По-
лучаем новую маркировку
'
= (
,
t
k
). Напомним, что маркировки мы
отождествляем с векторами. Ясно, что
'
=
–
a
k
+
b
k
.
Следовательно, работа маркированной сети Петри (раньше мы
записали эту работу в виде (1)) может быть записана в виде цепочки
векторов с целыми неотрицательными координатами:
1 (1)
2
,
;
, ...,
i
t
(2)
где
k+
1
=
k
–
a
i
(
k
)
+
b
i
(
k
)
и
k
a
i
(
k
)
при
k
= 1, … (Поясним, что нера-
венство
u
v
для двух векторов
u
,
v
означает, что
u
i
v
i
для всех
i
.)
Здесь
i
(
k
) есть номер активной позиции, переводящей
k
в
k+
1
.
0,1
1,0
t
t
Рис. 13
(1,0)
(
0,1)
(0,1)
(1,0)
(1,0)
t
1
t
t
1
t
2
t
t
2
Рис. 12
(1,0)
(
0,1)


