Н.В. Золотова, Р.С. Исмагилов
2
задачам; при этом описываются они весьма просто и наглядно. В каче-
стве примера избрали теорию сетей Петри. Такой выбор является до-
статочно естественным, ибо в последние десятилетия сети Петри про-
никают в разные области знания как весьма действенный инструмент
для описания сложных систем взаимодействующих объектов. Доста-
точно подробное изложение этой теории дано, например, в книгах
[3, 8, 9]. Разумеется, в статье идет речь только об основных понятиях
этой теории, однако это изложение может служить основой для даль-
нейшего изучения предмета, а также для внеаудиторных занятий сту-
дентов.
1. Сети Петри.
Возникли в 1962 г., и основной областью их приме-
нения являлись вычислительные системы. Эти системы, как правило,
состоят из многих компонент, имеющих многообразные и сложные вза-
имные связи. Оказалось, сети Петри — это удобный способ обозреть
эти связи. В дальнейшем сети Петри нашли применение также для ана-
лиза других сложных систем. Ниже (в разд. 6) приведен пример (разу-
меется, чрезвычайно простой) подобного применения.
Что такое сеть Петри? Это есть (по определению) ориентирован-
ный граф со следующими свойствами: его вершины разбиты на два
непересекающихся множества
P
,
T
, и каждое (ориентированное) ребро
идет от вершины, принадлежащей одному из этих множеств, к вер-
шине, лежащей в другом. Вершины из множества
P
называются пози-
циями и изображаются кружками, вершины из
T
называются перехо-
дами и изображаются палочками; (буквы
P
и
T
— от английских слов
position и transition). Позиции обозначаются через
p
i
, а переходы —
через
t
k
; здесь
i
,
k
— это номера позиций и переходов. От позиции к
переходу (и от перехода к позиции) могут вести несколько ребер. По-
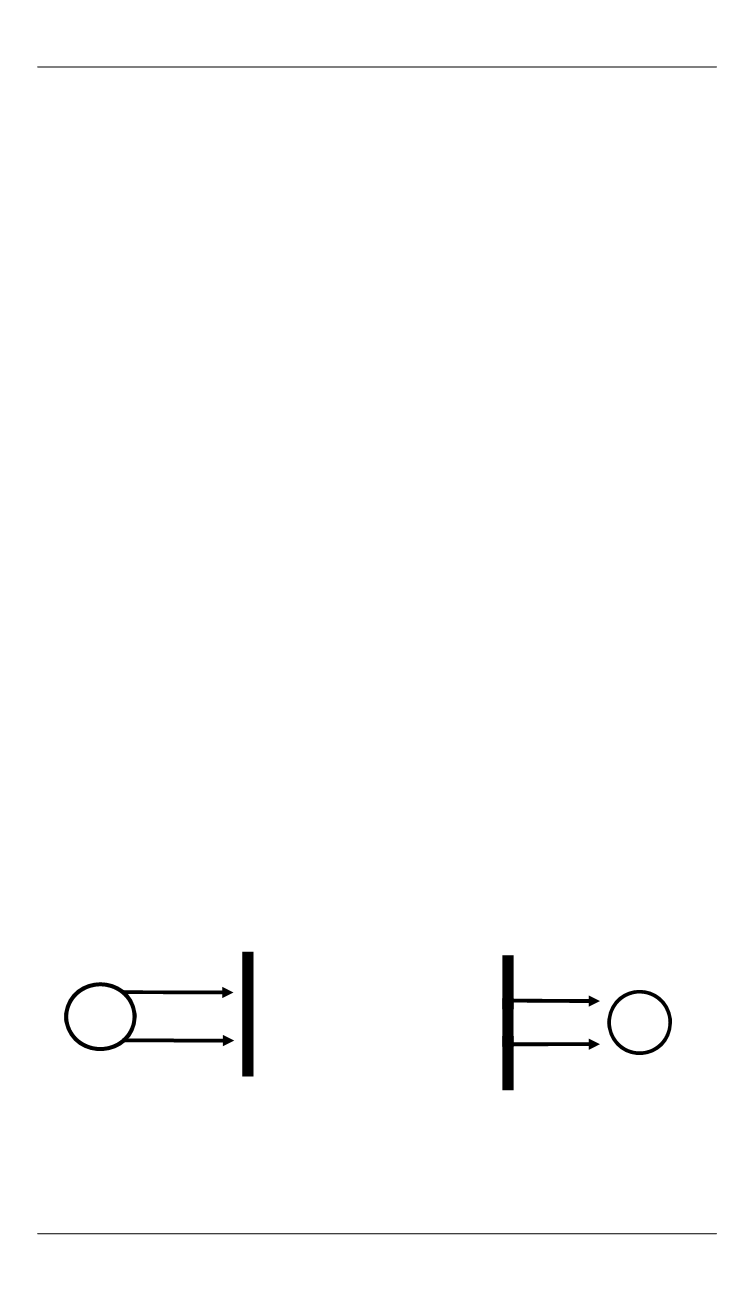
зиция, изображенная на рис. 1, называется входящей в переход
t
1
,
а позиция на рис. 2 — выходящей из перехода
t
1
. Одна и та же позиция
может быть как входной, так и выходной. На рис. 3 показан пример
сети Петри.
p
1
t
1
Позиция
Переход
Рис. 1
p
1
t
1
Рис. 2
Переход
Позиция


