Б.А. Унаспеков, К.О. Сабденов, В.Е. Зарко, М. Ерзада, Б.А. Игембаев
4
жидкой и газовой фаз обозначены как
ρ
f
,
ρ
g
);
η
— смещение поршня
от начального положения (рис. 2);
ξ
— изменение уровня жидкости;
k
— жесткость пружины 5 (см. рис. 1);
S
— площадь сечения каме-
ры 1 (или площадь поршня).
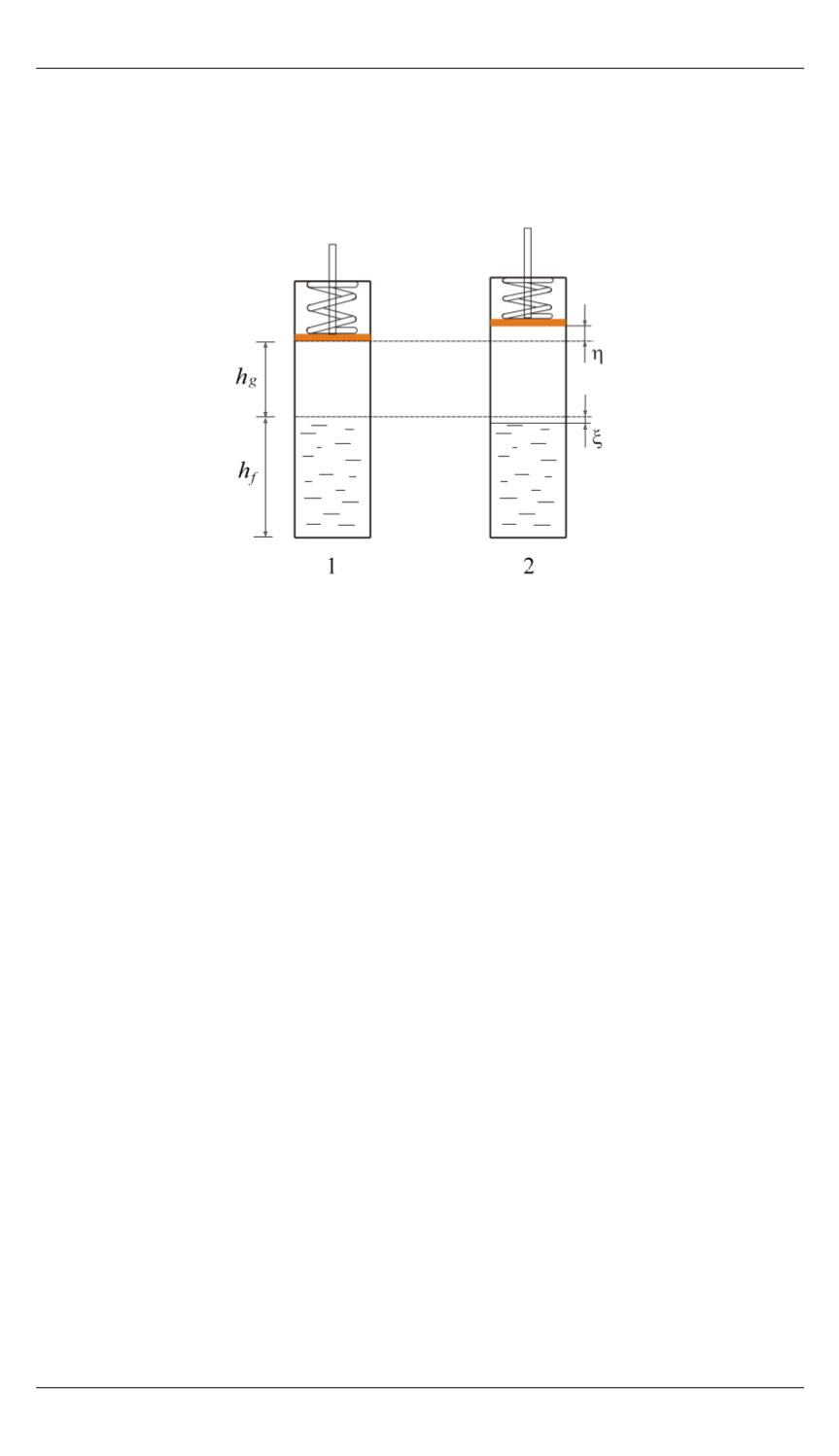
Рис. 2.
Положение поршня и уровень жидкой фазы в состояниях 1 и 2
Координата поверхности раздела фаз
x
s
=
h
f
–
ξ
, координата
поршня
x
p
=
h
f
+
h
g
+
η
, где
h
f
,
h
g
— протяженности областей, занятых
жидкой и газовой фазами. Положения сосредоточенных поверхно-
стей раздела фаз и поршня фиксируются дельта-функциями с аргу-
ментами
x
–
x
s
и
x
–
x
p
. Мощность тепла, поступающего в камеру
извне, обозначена как
W
, Дж/(м
3
⋅
с).
Плотность
ρ
и теплоемкость
c
претерпевают разрыв в точке
x
=
x
s
фазового превращения и определяются как
,
;
,
.
f f
s
p g
s
c
x x
c
c
x x
ρ ≤
⎧
ρ =
⎨
ρ >
⎩
.
Полагаем, что камера 1 может находиться в тепловом контакте
только с объектом
A
посредством теплообменника (площадь кон-
такта
S
a
) и с окружающей средой (воздухом) (площадь контакта
S
1
).
Тогда, если изменение температур
T
a
и
T
st
во времени происходит
значительно медленнее, чем при испарении и установлении термо-
динамических параметров в камере, температуру
T
в камере опре-
деляют через площади
S
a
и
S
1
и температуры
T
a
и
T
st
. Кроме того,
при незначительных перепадах температур
T
a
и
T
st
объем испаряю-
щейся или конденсирующейся жидкости мал:
ξ
<<
h
f
. Аналогичные
рассуждения применимы и к процессам в камере компенсатора. Все
это позволяет при моделировании регулятора ограничиться следую-
щими уравнениями:


