5
Следящий пневмопривод с цифровым управлением
тическим процессами. Уравнение состояния газа получим путем за-
мены показателя адиабаты
k
в адиабатическом процессе на показатель
политропы
n
:
pV
n
m
= RT
.
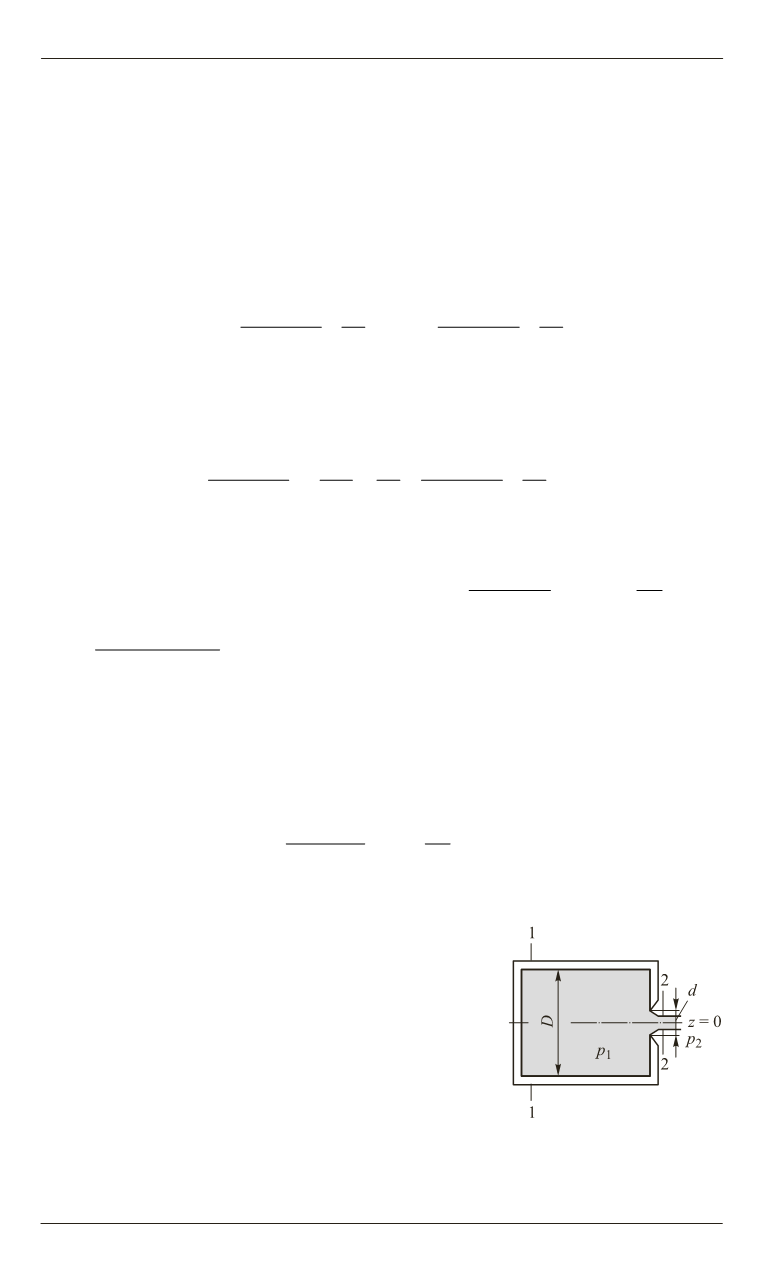
Для определения закона истечения газа в адиабатическом процессе
запишем уравнение Бернулли для сечений 2—2 потока, вытекающего
из пневматической емкости постоянного объема в газовую среду с дав-
лением
p
2
через круглое отверстие с заостренной кромкой (рис. 3):
2
2
1
1
2
2
1
2
1
2
,
1 2
1 2
kp u
kp u
gz
gz
k
k
после преобразований имеем
2 2
2
1
2
2
2
1
1
2
,
1
2
1 2
kp
s
u
kp u
k
k
где
s
= (
d
/
D
)2;
и
— скорость струи,
2/
1
2 2
1
1
2
1
1
k
k p
p
u
s
k
p
0,5
2
1 /
2 1
1
/
.
k k
p
p p
При истечении газа из пневматической емкости большого диамет-
ра (
D >> d
) и при
s
→ 0 скорость струи определяется по уравнению
Сен-Венана — Ванцеля:
0,5
( 1)/
1
2
1
1
2
1
1
.
k k
kp
p
u
k
p
(3)
В газодинамике широко используется от-
носительное давление β =
р
2
/
р
1
, которое далее
будем рассматривать как показатель критич-
ности процесса истечения сжатого воздуха в
газовую среду с абсолютным давлением
p
2
.
Процесс истечение воздуха как реального газа
происходит с потерями энергии, обусловлен-
ными обменом количества движения между
молекулами на уровне их взаимных соударе-
ний, которые учитываются коэффициентом
скорости φ и коэффициентом сжатия струи ε:
Рис. 3.
Расчетная схема
процесса истечения газа
через отверстие


