
В.В. Горский, А.А. Дмитриева
8
Инженерный журнал: наука и инновации
# 12·2017
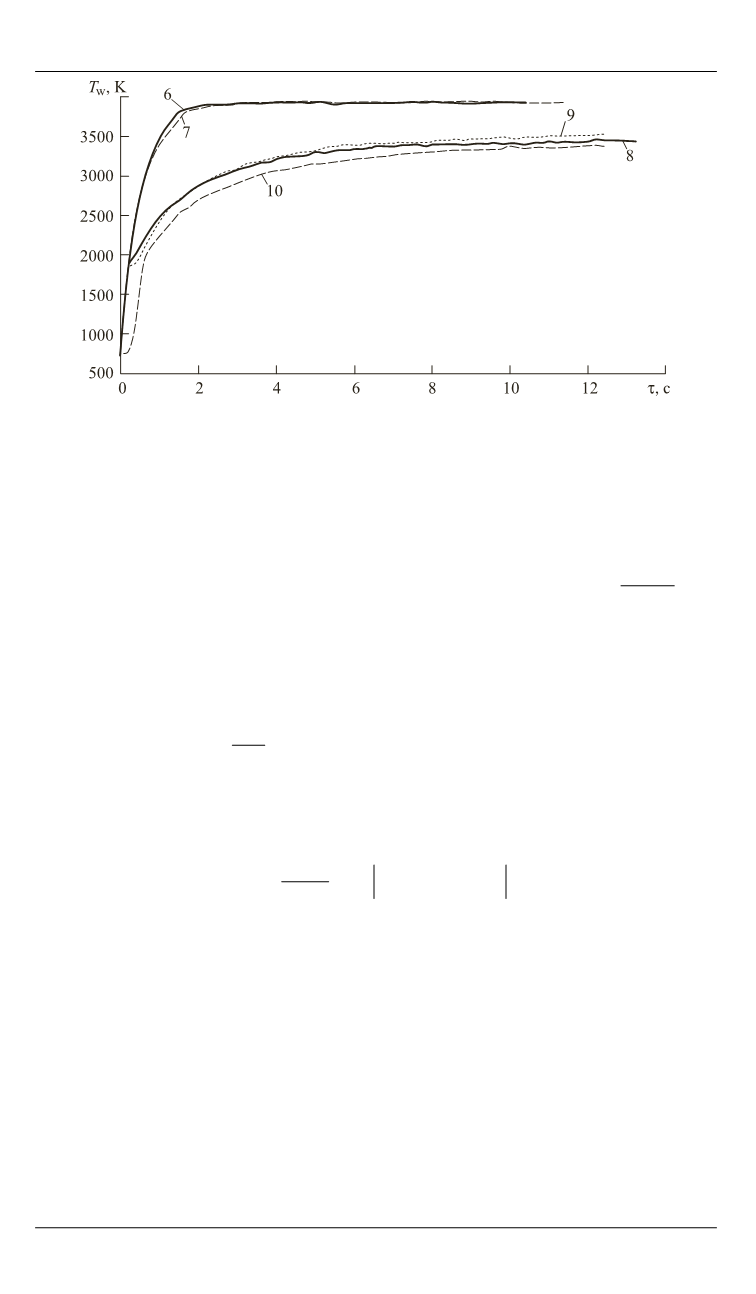
Рис. 3.
Зависимость температуры стенки в окрестности критической точки образца
от временной координаты (цифры над кривыми — номер эксперимента)
Если для каждого
k
-го эксперимента из числа эксперимен-
тов
Exp
N
установлены давление на модели
,
k
p
коэффициент тепло-
обмена
h,im,
k
A
на непроницаемой стенке, табличные зависимо-
сти
w, ,
,
j k
T
соответствующие временным шкалам
,
,
j k
,
1,
,
k
j
N
то
любому заданному набору искомых кинетических коэффициентов
может быть поставлено в соответствие расчетное значение обгара
материала в миллиметрах, рассчитываемого по формуле
3 ,
Cal,
Ox, 1
Ox,
1
2
10
/ 2.
N k
k
j
j
j
j
j
G G
Тогда в качестве критерия оптимальности искомого решения за-
дачи можно использовать минимум функционала
Exp
Cal,
Exp,
1
Exp
.
1
N
k
k
k
F
N
Решение сформулированной оптимизационной задачи проводит-
ся с помощью одного из вариантов эвристического метода прямого
поиска Хука — Дживса.
Пример решения оптимизационной задачи по определению
кинетических констант гетерогенного окисления углерода.
Ниже
проиллюстрирована возможность применения сформулированного
выше интегрального метода для определения кинетических констант,
входящих в уравнение (1), аппроксимирующее зависимость скорости
окисления углерода от температуры стенки. Используются необхо-
димые для применения данного метода экспериментальные данные
по зависимости температуры стенки в окрестности критической
















